References

International Journal of Applied Mathematics and Machine Learning

THE SECOND MULTIPLICATIVE ZAGREB ECCENTRICITY INDEX OF CIRCUMCORONENE SERIES OF BENZENOID

[1] D. B. West, An Introduction to Graph Theory, Prentice-Hall, 1996.

[2] A. T. Balaban (Ed.), From Chemical Topology to Three-dimensional Geometry, Plenum, New York, 1997.

[3] R. Todeschini and V. Consonni, Handbook of Molecular Descriptors, Wiley, Weinheim, 2000.

[4] I. Gutman and N. Trinajstić, Graph theory and molecular orbitals, III, Total 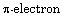energy of alternant hydrocarbons, Chem. Phys. Lett. 17 (1972), 535-538.

[5] I. Gutman and K. C. Das, The first Zagreb index 30 years after, MATCH Commun. Math. Comput. Chem. 50 (2004), 83-92.

[6] R. Todeschini and V. Consonni, New local vertex invariants and molecular descriptors based on functions of the vertex degrees, MATCH Commun. Math. Comput. Chem. 64 (2010), 359-372.

[7] R. Todeschini, D. Ballabio and V. Consonni, Novel molecular descriptors based on functions of the vertex degrees, in: I. Gutman and B. Furtula (Eds.), Novel Molecular Structure Descriptors-Theory and Applications I, Univ. Kragujevac, Kragujevac, (2010), 73-100.

[8] I. Gutman, Multipicative Zagreb indices of trees, Bull. Internat. Math. Virt. Inst. 1 (2011), 13-19.

[9] M. Ghorbani and M. A. Hosseinzadeh, A new version of Zagreb indices, Filomat 26(1) (2012), 93-100.

[10] D. Vukicevic and A. Graovac, Note on the comparison of the first and second normalized Zagreb eccentricity indices, Acta Chim. Slov. 57 (2010), 524-528.

[11] S. Sardana and A. K. Madan, MATCH Commun. Math. Comput. Chem. 43(85) (2001).

[12] S. Gupta, M. Singh and A. K. Madan, J. Math. Anal. Appl. (2002), 266-259.

[13] B. Furtula, A. Graovac and D. Vukičević, Disc. Appl. Math. 157 (2009), 2828.

[14] N. De, On multiplicative Zagreb eccentricity indices, South Asian J. Math. 2(6) (2012), 570-577.

[15] Z. Du, B. Zhou and N. Trinajstic, Extremal properties of the Zagreb eccentricity indices, Croat. Chem. Acta 85(3) (2012), 359-362.

[16] K. C. Das, D. W. Lee and A. Graovac, Some properties of the Zagreb eccentricity indices, Ars Math. Contemp. 6 (2013), 117-125.

[17] K. Xu and H. Hua, A united approach to extremal multiplicative Zagreb indices for trees, unicyclic and bicyclic graphs, MATCH Commun. Math. Comput. Chem. 68 (2012), 241-256.

[18] J. Liu and Qianhong Zhang, Sharp upper bounds for multiplicative Zagreb indices, MATCH Commun. Math. Comput. Chem. 68 (2012), 231-240.

[19] T. Reti and I. Gutman, Relations between ordinary and multiplicative Zagreb indices, Bull. Internat. Math. Virt. Inst. 2 (2012), 133-140.

[20] Z. Luo and J. Wu, Multiplicative Zagreb eccentricity indices of some composite graphs, Trans. Comb. 3(2) (2014), 21-29.

[21] H. Wang and H. Bao, A note on multiplicative sum Zagreb index, South Asian J. Math. 2(6) (2012), 578-583.

[22] M. R. Farahani, Multiplicative versions of Zagreb indices of Journal of Chemistry and Materials Research 2(2) (2015), 67-70.

[23] M. R. Farahani, On multiple Zagreb indices of dendrimer nanostars, International Letters of Chemistry, Physics and Astronomy 52 (2015), 147-151.

[24] M. R. Farahani, On multiple Zagreb indices of circumcoronene homologous series of benzenoid, Chemical Physics Research Journal 7(2) (2014), 277-282.

[25] V. Chepoi and S. Klavžar, Distances in benzenoid systems: Further developments, Discrete. Math. 192 (1998), 27-39.

[26] S. Klavžar and I. Gutman, Bounds for the Schultz molecular topological index of benzenoid systems in terms of Wiener index, J. Chem. Inf. Comput. Sci. 37(4) (1997), 741-744.

[27] S. Klavžar, A bird s eye view of the cut method and a survey of its applications in chemical graph theory, MATCH Commun. Math. Comput. Chem. 60 (2008), 255-274.

[28] P. E. John, P. V. Khadikar and J. Singh, A method of computing the PI index of benzenoid hydrocarbons using orthogonal cuts, J. Math. Chem. 42(1) (2007), 27-45.

[29] S. Klavžar, I. Gutman and B. Mohar, Labeling of benzenoid systems which reflects the vertex-distance relations, J. Chem. Inf. Comput. Sci. 35 (1995), 590-593.

[30] S. Klavžar and I. Gutman, A comparison of the Schultz molecular topological index with the Wiener index, J. Chem. Inf. Comput. Sci. 36 (1996), 1001-1003.

[31] K. Salem, S. Klavžar and I. Gutman, On the role of hyper-cubes in the resonance graphs of benzenoid graphs, Discrete Math. 13(8) (2003), 306.

[32] P. Zigert, S. Klavžar and I. Gutman, Calculating the hyper-Wiener index of benzenoid hydrocarbons, ACH Models Chem. 137 (2000), 83-94.

[33] M. R. Farahani, Computing first-, second -connectivity index and first-, second-sum-connectivity index of circumcoronene series of benzenoid, Pacific Journal of Applied Mathematics 6(4) (2014).

[34] M. R. Farahani, A new version of Zagreb index of circumcoronene series of benzenoid, Chemical Physics Research Journal 6(1) (2013), 27-33.

[35] M. R. Farahani, Third-connectivity and third-sum-connectivity indices of circumcoronene series of benzenoid Acta Chim. Slov. 60 (2013), 198-202.

[36] M. R. Farahani, Computing eccentricity connectivity polynomial of circumcoronene series of benzenoid by ring-cut method, Annals of West University of Timisoara-Mathematics and Computer Science 51(2) (2013), 29-37.