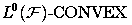International Journal of Applied Mathematics and Machine Learning
CONES IN COMPLETE RANDOM NORMED MODULESAuthor's: Yujie Yang
Pages: [73] - [87]
Received Date: June 6, 2019
Submitted by: Jianqiang Gao.
DOI: http://dx.doi.org/10.18642/ijamml_7100122072
Based on the previous results, this paper continues to develop the
theory of random convex analysis. First, motivated by the recent work
of Ekeland’s variational principle on a complete random normed
module, we prove that the set of local conical support points of
S is dense in the boundary of S under the locally
topology, where S is a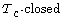 
subset of a random normed module E and
S has the countable concatenation property. Then, we prove that
it is a nonconvex generalization of the Bishop-Phelps theorem in
complete random normed modules. This result is a nontrivial random
extension of the corresponding classic result.
random normed module, locally topology, closed set, Bishop-Phelps theorem.
