International Journal of Applied Mathematics and Machine LearningAuthor's: Bachir Dehda and Khaled Melkemi
Pages: [43] - [65]
Received Date: July 21, 2016; Revised August 17, 2016
Submitted by: Hind Rustum Mohammed Shaaban.
DOI: http://dx.doi.org/10.18642/ijamml_7100121693
In this paper, we present a new method for images compression, which
is based on a reduction of the wavelet coefficients number
independently of the singularity contained in the images. This method,
called the hybridization of detail space (HDS), compared to discrete
wavelet transform (DWT), it has many advantages. The (HDS) method
considers first an r-regular multiresolution analysis
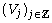of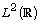 
and replaces a great number of its
wavelet basis elements by new vectors using the orthogonal matrices
and prime numbers. So, it can make a great number of wavelet
coefficients be equal to zero independently of the image singularity.
For illustrating the effectiveness of the (HDS) method compared to
(DWT), we have implemented the algorithm on a gray-scale image that
has considerable singularities in MATLAB, and the decomposition has
been done at level 
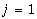using Haar wavelet. So, the experimental
results with this new method have given the better performance for the
quality and the size of the compressed image.
wavelets, multiresolution analysis, hybridization of detail space, image compression and denoising.
