Journal of Pure and Applied Mathematics: Advances and Applications[1] R. P. Agarwal, N. J. Huang and M. Y. Tan, Sensitivity analysis for
a new system of generalized nonlinear mixed quasi-variational
inclusions, Applied Mathematics Letters 17(3) (2004), 345-352.
[2] K. Aoyama, H. Iiduka and W. Takahashi, Weak convergence of an
iterative sequence for accretive operators in Banach spaces, Fixed
Point Theory and Applications, Volume 2006, Article ID 35390, Pages
1-13.
[3] K. Ball, E. A. Carlen and E. H. Lieb, Sharp uniform convexity and
smoothness inequalities for trace norms, Inventions Mathematica 115(3)
(1994), 463-482.
[4] V. Barbu, Nonlinear Semi-groups and Differential Equations in
Banach Spaces, Noordhoff, 1976.
[5] S. S. Chang, H. W. Joseph and C. K. Chan, Generalized system for
relaxed cocoercive variational inequalities in Hilbert spaces,
Applied Mathematics Letters 20(3) (2007), 329-334.
[6] Y. J. Cho and X. Qin, System of generalized nonlinear variational
inequalities and its projection methods, Nonlinear Analysis: Theory,
Methods and Applications 69(12) (2008), 4443-4451.
[7] Y. J. Cho, S. M. Kang and X. Qin, On systems of generalized
nonlinear variational inequalities in Banach spaces, Applied
Mathematics and Computation 206(1) (2008), 214-220.
[8] J. Fan, A Mann type iterative scheme for variational inequalities
in noncompact subsets of Banach spaces, Journal of Mathematical
Analysis and Applications 337(2) (2008), 1041-1047.
[9] Y. P. Fang and N. J. Huang, Iterative algorithm for a system of
variational inclusions involving H-accretive operators in
Banach spaces, Acta Mathematica Hungarica 108(3) (2005), 183-195.
[10] C. He, Three-step projection methods and iterative approximation
for a class of systems of variational inequalities, Nonlinear
Functional Analysis and Applications 13(5) (2008), 781-787.
[11] Z. Y. Huang and M. A. Noor, An explicit projection method for a
system of nonlinear variational inequalities with different
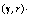cocoercive mappings, Applied Mathematics and
Computation 190(1) (2007), 356-361.
[12] H. Y. Lan, Nonlinear parametric multi-valued variational
inclusion systems involving (A,)-accretive mappings in Banach
spaces, Nonlinear Analysis: Theory, Methods and Applications 69(5-6)
(2008), 1757-1767.
[13] S. Reich, Asymptotic behavior of contractions in Banach spaces,
Journal of Mathematical Analysis and Applications 44(1) (1973), 57-70.
[14] Y. Takahashi, K. Hashimoto and M. Kato, On sharp uniform
convexity, smoothness, and strong type, cotype inequalities, Journal
of Nonlinear and Convex Analysis 3(2) (2002), 267-281.
[15] R. U. Verma, Projection methods, algorithms and a new system of
nonlinear variational inequalities, Computers and Mathematics with
Applications 41(7-8) (2001), 1025-1031.
[16] R. U. Verma, Generalized class of partial relaxed monotonicity
and its connections, Advances in Nonlinear Variational Inequalities
7(2) (2004), 155-164.
[17] R. U. Verma, Generalized system for relaxed cocoercive
variational inequalities and projection methods, Journal of
Optimization Theory and Applications 121(1) (2004), 203-210.
[18] R. U. Verma, General convergence analysis for two-step projection
methods and application to variational problems, Applied Mathematics
Letters 18(11) (2005), 1286-1292.
[19] H. K. Xu, Inequalities in Banach spaces with applications,
Nonlinear Analysis: Theory, Methods and Applications 16(12) (1991),
1127-1138.
