Journal of Pure and Applied Mathematics: Advances and Applications[1] R. A. Adams, Sobolev Spaces, Academic Press, New York, 1975.
[2] T. Arbogast and M. F. Wheeler, A characteristics-mixed finite
element method for advection-dominated transport problems, SIAM
Journal on Numerical Analysis 32(2) (1995), 404-424.
DOI: https://doi.org/10.1137/0732017
[3] J. B. Bell, C. N. Dawson and G. R. Shubin, An unsplit, higher
order Godunov method for scalar conservation laws in multiple
dimensions, Journal of Computational Physics 74(1) (1988), 1-24.
DOI: https://doi.org/10.1016/0021-9991(88)90065-4
[4] Z. Cai, On the finite volume element method, Numerische Mathematik
58(1) (1990), 713-735.
DOI: https://doi.org/10.1007/BF01385651
[5] Z. Cai, J. E. Jones, S. F. McCormick and T. F. Russell,
Control-volume mixed finite element methods, Computational Geosciences
1(3-4) (1997), 289-315.
DOI: https://doi.org/10.1023/A:1011577530905
[6] M. A. Cella, T. F. Russell, I. Herrera and R. E. Ewing, An
Eulerian-Lagrangian localized adjoint method for the
advection-diffusion equation, Advances in Water Resources 13(4)
(1990), 187-206.
DOI: https://doi.org/10.1016/0309-1708(90)90041-2
[7] P. G. Ciarlet, The Finite Element Method for Elliptic Problems,
North Holland, Amsterdam, 1978.
[8] S. H. Chou, D. Y. Kwak and P. S. Vassilevski, Mixed covolume
methods for elliptic problems on triangular grids, SIAM Journal on
Numerical Analysis 35(5) (1998), 1850-1861.
DOI: https://doi.org/10.1137/S0036142997321285
[9] S. H. Chou and P. S. Vassilevski, A general mixed covolume
framework for constructing conservative schemes for elliptic problems,
Mathematics of Computation 68(227) (1999), 991-1011.
DOI: https://doi.org/10.1090/S0025-5718-99-01090-X
[10] S. H. Chou and D. Y. Kwak, Mixed covolume methods on rectangular
grids for elliptic problems, SIAM Journal on Numerical Analysis 37(3)
(2000), 758-771.
DOI: https://doi.org/10.1137/S0036142996305534
[11] C. N. Dawson, T. F. Russell and M. F. Wheeler, Some improved
error estimates for the modified method of characteristics, SIAM
Journal on Numerical Analysis 26(6) (1989), 1487-1512.
DOI: https://doi.org/10.1137/0726087
[12] C. N. Dawson, C. J. Van Duijn and M. F. Wheeler,
Characteristic-Galerkin methods for contaminant transport with
nonequilibrium adsorption kinetics, SIAM Journal on Numerical Analysis
31(4) (1994), 982-999.
DOI: https://doi.org/10.1137/0731052
[13] C. N. Dawson, Analysis of an upwind-mixed finite element method
for nonlinear contaminant transport equations, SIAM Journal on
Numerical Analysis 35(5) (1998), 1709-1724.
DOI: https://doi.org/10.1137/S0036142993259421
[14] J. Douglas Jr., Simulation of miscible displacement in porous
media by a modified method of characteristic procedure, In Numerical
Analysis, Dundee, 1981; Lecture Notes in Mathematics, 912,
Springer-Verlag, Berlin, 1982.
DOI: https://doi.org/10.1007/BFb0093149
[15] J. Douglas Jr., R. E. Ewing and M. F. Wheeler, Approximation of
the pressure by a mixed method in the simulation of miscible
displacement, RAIRO Analyse Numérique 17(1) (1983), 17-33.
[16] J. Douglas Jr., R. E. Ewing and M. F. Wheeler, A
time-discretization procedure for a mixed finite element approximation
of miscible displacement in porous media, RAIRO Analyse Numérique
17(3) (1983), 249-265.
[17] R. E. Ewing, The Mathematics of Reservoir Simulation, SIAM,
Philadelphia, 1983.
[18] U. Hornung, Miscible Displacement in Porous Media Influenced by
Mobile and Immobile Water, Nonlinear Partial Differential Equations,
Springer, New York, 1988.
[19] R. H. Li and Z. Y. Chen, Generalized Difference of Differential
Equations, Jilin University Press, Changchun, 1994 (in Chinese).
[20] L. S. Jiang and Z. Y. Pang, Finite Element Method and its Theory,
People’s Education Press, Beijing, 1979 (in Chinese).
[21] C. Johnson, Streamline Diffusion Methods for Problems in Fluid
Mechanics, in Finite Element in Fluids VI, Wiley, New York, 1986.
[22] J. E. Jones, A Mixed Finite Volume Method for Accurate
Computation of Fluid Velocities in Porous Media, Ph. D. Thesis,
University of Colorado, Denver, Co., 1995.
[23] J. Nitsche, Linear splint-funktionen und die methoden von ritz
fur elliptishce randwertprobleme, Archive for Rational Mechanics and
Analysis 36(5) (1970), 348-355.
DOI: https://doi.org/10.1007/BF00282271
[24] H. Pan and H. X. Rui, Mixed element method for two-dimensional
Darcy-Forchheimer model, Journal of Scientific Computing 52(3) (2012),
563-587.
DOI: https://doi.org/10.1007/s10915-011-9558-3
[25] P. A. Raviart and J. M. Thomas, A Mixed Finite Element Method for
Second Order Elliptic Problems, in: Mathematical Aspects of the Finite
Element Method, Lecture Notes in Mathematics, 606, Springer-Verlag,
Berlin, 1977.
DOI: https://doi.org/10.1007/BFb0064470
[26] H. X. Rui and H. Pan, A block-centered finite difference method
for the Darcy-Forchheimer model, SIAM Journal on Numerical Analysis
50(5) (2012), 2612-2631.
DOI: https://doi.org/10.1137/110858239
[27] T. F. Russell, Rigorous Block-Centered Discretizations on
Irregular Grids: Improved Simulation of Complex Reservoir Systems,
Project Report, Research Corporation, Tulsa, 1995.
[28] P. P. Shen, M. X. Liu and L. Tang, Mathematical Model of
Petroleum Exploration and Development, Science Press, Beijing, 2002
(in Chinese).
[29] T. J. Sun and Y. R. Yuan, An approximation of incompressible
miscible displacement in porous media by mixed finite element method
and characteristics-mixed finite element method, Journal of
Computational and Applied Mathematics 228(1) (2009), 391-411.
DOI: https://doi.org/10.1016/j.cam.2008.09.029
[30] M. R. Todd, P. M. O’Dell and G. J. Hirasaki, Methods for
increased accuracy in numerical reservoir simulators, Society of
Petroleum Engineers Journal 12(6) (1972), 521-530.
DOI: https://doi.org/10.2118/3516-PA
[31] C. H. Vogt, A Homogenization Theorem Leading to a Volterra
Integro-Differential Equation for Permeation Chromotography, SFB 123,
Preprint 155, Heidelberg, SFB-Preprints, 1982.
[32] A. Weiser and M. F. Wheeler, On convergence of block-centered
finite differences for elliptic problems, SIAM Journal on Numerical
Analysis 25(2) (1988), 351-375.
DOI: https://doi.org/10.1137/0725025
[33] D. P. Yang, Analysis of least-squares mixed finite element
methods for nonlinear nonstationary convection-diffusion problems,
Mathematics of Computation 69(231) (2000), 929-963.
DOI: https://doi.org/10.1090/S0025-5718-99-01172-2
[34] Y. R. Yuan, Characteristic finite element methods for positive
semidefinite problem of two phase miscible flow in three dimensions,
Science Bulletin China 41(22) (1996), 2027-2032 (in Chinese).
[35] Y. R. Yuan, Characteristic finite difference methods for positive
semidefinite problem of two phase miscible flow in porous media,
Journal of Systems Science and Mathematical Sciences 12(4) (1999),
299-306.
[36] Y. R. Yuan, Theory and Application of Reservoir Numerical
Simulation, Science Press, Beijing, 2013 (in Chinese).
[37] U. Khan, R. Ellahi, R. Khan and S. T. Mohyud-Din, Extracting new
solitary wave solutions of Benny-Luke equation and Phi-4 equation of
fractional order by using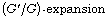 
method, Optical and Quantum Electronics 49
(2017), 1-14; Article 362.
DOI: https://doi.org/10.1007/s11082-017-1191-4
[38] W. Sikander, U. Khan, N. Ahmed and S. T. Mohyud-Din, Optimal
solutions for homogeneous and non-homogeneous equations arising in
physics, Results in Physics 7 (2017), 216-224.
DOI: https://doi.org/10.1016/j.rinp.2016.12.018
[39] W. Sikander, U. Khan and S. T. Mohyud-Din, Optimal solutions for
the evolution of a social obesity epidemic model, Eur. Phys. J. Plus
132(6) (2017), 257.
[40] S. T. Mohyud-Din, A. Irshad, N. Ahmed and U. Khan, Exact
solutions of 
generalized KP equation arising in physics,
Results in Physics 7 (2017), 3901-3909.
DOI: https://doi.org/10.1016/j.rinp.2017.10.007
[41] S. T. Mohyud-Din, M. A. Noor and K. I. Noor, Some relatively new
techniques for nonlinear problems, Mathematical Problems in
Engineering (2009), 25 pages; Article ID 234849.
DOI: http://dx.doi.org/10.1155/2009/234849
[42] S. T. Mohyud-Din, A. Yildirim and G. Demirli, Analytical solution
of wave system in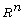 
with coupling controllers, International
Journal of Numerical Methods for Heat & Fluid Flow 21(2) (2011),
198-205.
DOI: https://doi.org/10.1108/09615531111105399
[43] S. T. Mohyud-Din, A. Yildirim and S. Sariaydin, Numerical soliton
solution of the Kaup-Kupershmidt equation, International Journal of
Numerical Methods for Heat & Fluid Flow 21(3) (2011), 272-281.
DOI: https://doi.org/10.1108/09615531111108459
[44] J. H. He, Generalized variational principles for buckling
analysis of circular cylinders, Acta Mechanica (2019), 1-8.
DOI: https://doi.org/10.1007/s00707-019-02569-7
[45] J. H. He, Variational principle for the generalized KdV-Burgers
equation with fractal derivatives for shallow water waves, Journal of
Applied and Computational Mechanics 6(4) (2020).
DOI: https://doi.org/10.22055/JACM.2019.14813
[46] J. H. He, A modified Li-He’s variational principle for
plasma, International Journal of Numerical Methods for Heat and Fluid
Flow (2019).
DOI: https://doi.org/10.1108/HFF-06-2019-0523
[47] J. H. He, Lagrange crisis and generalized variational principle
for 3D unsteady flow, International Journal of Numerical Methods for
Heat and Fluid Flow (2019).
DOI: https://doi.org/10.1108/HFF-07-2019-0577
[48] J. H. He and C. Sun, A variational principle for a thin film
equation, Journal of Mathematical Chemistry 57(9) (2019), 2075-2081.
DOI: https://doi.org/10.1007/s10910-019-01063-8
[49] C. H. He, Y. Shen, F. Y. Ji and J. H. He, Taylor series solution
for fractal Bratu-type equation arising in electrospinning process,
Fractals (2019).
DOI: https://doi.org/10.1142/S0218348X20500115
[50] H. Y. Liu, S. W. Yao, H. W. Yang and F. J. Liu, A fractal rate
model for adsorption kinetics at solid/solution interface, Thermal
Science 23(4) (2019), 2477-2480.
DOI: https://doi.org/10.2298/TSCI1904477L
[51] Q. L. Wang, X. Y. Shi, J. H. He and Z. B. Li, Corrigendum:
Fractal calculus and its application to explanation of biomechanism of
polar bear hairs, Fractals 27(5) (2019); Article 1992001.
DOI: https://doi.org/10.1142/S0218348X19920014
[52] Y. Wang, S. W. Yao and H. W. Yang, A fractal derivative model for
snow’s thermal insulation property, Thermal Science 23(4)
(2019), 2351-2354.
DOI: https://doi.org/10.2298/TSCI1904351W
