Journal of Pure and Applied Mathematics: Advances and Applications[1] E. R. Berlekamp, J. H. Conway and R. K. Guy, Winning Ways for Your
Mathematical Plays, A. K. Peters, Wellesley, MA, 2004.
[2] J. H. Conway, On Numbers and Games, CRC Press, 2000.
[3] E. Duchêne, A. S. Fraenkel, R. J. Nowakowski and M. Rigo,
Extensions and restrictions of Wythoff’s game preserving its
P-positions, J. Combin. Theory Ser. A 117 (2010), 545-567.
[4] A. S. Fraenkel, Scenic trails ascending from sea-level Nim to
alpine chess, in: R. J. Nowakowski (Ed.), Games of No Chance, Proc.
MSRI Workshop on Combinatorial Games, July, 1994, Berkely, CA, MSRI
Publ., Vol. 29, Cambridge University Press, Cambridge, (1996),
13-42.
[5] A. S. Fraenkel, Heap games, numeration systems and sequences, Ann.
Comb. 2 (1998), 197-210.
[6] A. S. Fraenkel and M. Ozery, Adjoining to Wythoff’s game its
P-positions as moves, Theoret. Comput. Sci. 205 (1998),
283-296.
[7] A. S. Fraenkel, Wythoff games, continued fractions, cedar trees
and Fibonacci searches, Theoret. Comput. Sci. 29(1-2) (1984),
49-73.
[8] A. S. Fraenkel and M. Lorberbom, Nimhoff games, J. Combin. Theory
Ser. A 58 (1991), 1-25.
[9] A. S. Fraenkel and Y. Tanny, A class of Wythoff-like games, Proc.
INTEGERS Conference, Carrollton, Georgia, Oct. 26-29, 2011, in:
INTEGERS, Electr. J. Combinat. Number Theory 12(B) (2013), 
[10] W. A. Liu, Y. Wang and N. Li, The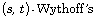 
game under misère play convention, Fifth
International Joint Conference on Computational Sciences and
Optimization, Harbin, China (2012), 419-422.
[11] W. A. Liu and X. Zhao, Adjoning to 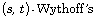game its P-positions as moves,
Discret. Appl. Math. 179 (2014), 28-43.
[12] W. Wythoff, A modification of the game of Nim, Nieuw Arch. Wiskd.
7 (1907), 199-202.
