Journal of Pure and Applied Mathematics: Advances and Applications[1] M. A. Arcones, The Bahadur-Kiefer representation of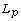 
regression estimayors, Econometric Theory
12 (1996), 257-283.
[2] R. Azrak and G. Melard, Asymptotic properties of quasi-maximum
likelihood estimators for ARMA models with time-dependent
coefficients, Statistical Inference for Stochastic Processes 9 (2006),
279-330.
[3] F. Carsoule and P. H. Franses, A note on monitoring time-varying
parameters in an autoregression, Metrika 57 (2003), 51-62.
[4] P. W. Douglas, Asymptotics of generalized M-estimation of
regression and scale with fixed carriers, in an approximately linear
model, Statistics & Probability Letters 30 (1996), 271-285.
[5] H. C. Hu, QML estimators in linear regression models with
functional coefficient autoregressive processes, Mathematical Problems
in Engineering, Volume 2010. Article ID 956907,
doi:10.1155/2010/956907, 1-30.
[6] G. H. Kwoun and Y. Yajima, On an autoregressive model with
time-dependent coefficients, Annals of the Institute of Statistical
Mathematics 35 (1986), 297-309.
[7] R. A. Maller, Asymptotics of regressions with stationary and
nonstationary residuals, Stochastic Processes and their Applications
105 (2003), 33-67.
[8] P. Pere, Adjusted estimates and Wald statistics for the AR(1)
model with constant, Journal of Econometrics 98 (2000), 335-363.
[9] A. E. Rouner, Asymptotic normality of P-norm estimators in
multiple regression, Wahrschrinlichkei-theorie und Verwandte Gebiete
66 (1984), 620-631.
[10] M. J. Silvapulle, Asymptotic behavior of robust estimators of
regression and scale parameters with fixed carriers, The Annals of
Statistics 13(4) (1985), 1490-1497.
[11] L. Song, H. C. Hu and X. S. Cheng, Hypothesis testing in
generalized models with functional coefficient autoregressiver
processes, Mathematical Problems in Engineering 2012.
http://dx.doi.org/10.1155/2012/862398
[12] X. W. Tong, H. J. Cui and P. Yu, Consistency and normality of
Huber-Dutter estimators for partial linear model, Science in China,
Series A: 51(10) (2008), 1831-1842.
