Journal of Pure and Applied Mathematics: Advances and Applications[1] N. Euler, Transformation properties of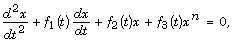 
Journal of Nonlinear Mathematical Physics 4
(1997), 310-337.
[2] R. Conte, Partial integrability of the anharmonic oscillator,
Journal of Nonlinear Mathematical Physics 14 (2007), 454-465.
[3] E. Fermi, Un metodo statistico par la determinazione di alcune
proprietà dell’atome, Rend. Accad. Naz. Lincei, Cl. Sci.
Fis. Mat. Nat. 6 (1927), 602-607.
[4] L. H. Thomas, The calculation of atomic fields, Proc. Cambridge
Phil. Soc. 13 (1927), 542-548.
[5] V. P. Ermakov, Équations differentielles du deuxième ordre.
Conditios d’intégrabilité sous forme finale, Univ. Izv.
Kiev 3 (1880), 1-25.
[6] E. Pinney, The nonlinear differential equation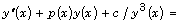 
0. Proc. Amer. Math. Soc. 1 (1950), 681.
[7] V. Bevc, J. L. Palmer and C. Süsskind, On the design of the
transition region of axi-symmetric magnetically focusing beam values,
J. British Inst. Radio Eng. 18 (1958), 696-708.
[8] P. J. Torres, Existence and uniqueness of elliptic periodic
solutions of the Brillouin electron beam focusing system, Math. Meth.
Appl. Sci. 23 (2000), 1139-1143.
[9] I. Kovacic and M. J. Brennan (Editors), The Duffing Equation:
Nonlinear Oscillators and their Behaviour, John Wiley & Sons,
Chichester, United Kingdom, 2011.
[10] P. B. Espinoza, Ermakov-Lewis dynamic invariants with some
applications, arXiv:math-ph/0002005 (2005).
[11] P. G. Kevrekidis and Y. Drossinos, Nonlinearity from linearity:
The Ermakov-Pinney equation revisited, Math. Computers in Simulation
74 (2007), 196-202.
[12] H. Rosu, P. Espinoza and M. Reyes, Ermakov approach for
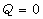empty FRW minisuperspace oscillators, Nuovo
Cim. B 114 (1999), 1439-1443.
[13] R. M. Hawkins and J. E. Lidsey, The Ermakov-Pinney equation in
scalar field cosmologies, Phys. Rev. D 66 (2002), 023523.
[14] F. Finelli, G. P. Vacca and G. Venturi, Chaotic inflation from a
scalar field in nonclassical states, Phys. Rev. D 58 (1998),
103514.
[15] C. Bertoni, F. Finelli and G. Venturi, Adiabatic invariants and
scalar fields in de Sitter space-time, Phys. Lett. A 237 (1998),
331-336.
[16] M. Shahinpoor and J. L. Nowinski, Exact solution to the problem
of forced large amplitude radial oscillations of a thin hyperelastic
tube, Int. J. Nonlinear Mech. 6 (1971), 193-207.
[17] A. M. Goncharenko, Yu. A. Logvin, A. M. Samson and P. S.
Shapovalov, Rotating elliptical Gaussian beams in nonlinear media,
Opt. Commun. 81 (1991), 225-230.
[18] A. M. Goncharenko, Yu. A. Logvin, A. M. Samson, P. S. Shapovalov
and S. I. Turovets, Ermakov Hamiltonian systems in nonlinear optics of
elliptic Gaussian, Phys. Lett. A 160 (1991), 138-142.
[19] C. J. Pethick and H. Smith, Bose-Einstein Condensation in Dilute
Gases, Cambridge University Press, Cambridge, 2001.
[20] Yu. S. Kivshar and G. P. Agrawal, Optical Solitons: From Fibers
to Photonic Crytals, Academic Press, Boston, 2003.
[21] J. J. Garcia-Ripoll, V. M. Pérez-Garcia and P. J. Torres,
Extended parametric resonances in nonlinear Schrödinger systems,
Phys. Rev. Lett. 83 (1999), 1715.
[22] G. D. Montesinos, V. M. Pérez-Garcia and P. J. Torres,
Stabilization of solitons of the multidimensional nonlinear
Schrödinger equation: Matter wave breathers, Physica D 191 (2004),
193-210.
[23] M. Centurion, M. A. Porter, P. G. Kevrekidis and D. Psaltis,
Nonlinearity management in optics: Experiment, theory and simulation,
Phys. Rev. Lett. 033903, 97 (2006).
[24] W. K. Schief, A discrete Pinney equation, Appl. Math. Lett. 10
(1997), 13-15.
[25] W. K. Schief, C. Rogers and A. P. Bassom, Ermakov systems of
arbitrary order and dimension: Structure and linearization, J. Phys. A
Math. Gen. 9 (1996), 903-911.
[26] A. N. W. Hone, Exact discretization of the Ermakov-Pinney
equation, Phys. Lett. A 263 (1999), 347-354.
[27] S. C. Mancas and H. C. Rosu, Ermakov-Pinney equations with
Abel-induced dissipation; arXiv:1301.3567 (2013).
[28] H.-C. Kim and J. H. Yee, Time-dependent driven anharmonic
oscillator and the adiabaticity, Phys. Rev. A 66 (2002), 032117.
[29] A. A. Zheltukhin, Toroidal p-branes, anharmonic oscillators and
(hyper) elliptic solutions, Nucl. Phys. B 858 (2012), 142-154.
[30] C. Bervillier, Conformal mappings versus other power series
methods for solving ordinary differential equations: Illustration on
anharmonic oscillators, J. Phys. A: Math. Theor. 42 (2009), 485202.
[31] P. Pedram, Anharmonic oscillator and the optimized basis
expansion, Applied Mathematics and Computation 219 (2013),
4655-4666.
[32] B. Gambier, Sur les équations diérentielles du second ordre
et du premier degré dont l’intégrale générale est a
points critique fixes, Acta Math. 33 (1910), 1-55.
[33] L. G. S. Duarte, I. C. Moreira and F. C. Santos, Linearisation
under nonpoint transformations, J. Phys. A: Math. Gen. 27 (1994),
L739-L743.
[34] N. Euler, T. Wolf, P. G. L. Leach and M. Euler, Linearisable
third order ordinary differential equations and generalized Sundman
transformations; arXiv:nlin/0203028 (2002).
[35] K. F. Sundman, Mé moire sur le problèm des trois corps,
Acta Mathematica 36 (1912), 105-179.
[36] M. Zhang, Periodic solutions of equations of Ermakov-Pinney type,
Advanced Nonlinear Studies 6 (2006), 57-67.
[37] P. Yan and M. Zhang, Higher order non-resonance for differential
equations with singularities, Math. Meth. Appl. Sci. 26 (2003),
1067-1074.
