Journal of Mathematical Sciences: Advances and Applications[1] L. M. Abia, J. C. López-Marcos and J. MartÃnez, On the
blow-up time convergence of semi-discretizations of reaction-diffusion
equations, Appl. Numer. Math. 26 (1998), 399-414.
[2] A. Acker and W. Walter, The quenching problem for nonlinear
parabolic differential equations, Lecture Notes in Math.,
Springer-Verlag, New York, 564 (1976), 1-12.
[3] A. Acker and B. Kawohl, Remarks on quenching, Nonl. Anal. TMA 13
(1989), 53-61.
[4] C. Bandle and C. M. Braumer, Singular perturbation method in a
parabolic problem with free boundary, in Proc. BAIL IVth Conference,
Boole Press Conf. Ser. 8, Novosibirsk (1986), 7-14.
[5] P. Baras and L. Cohen, Complete blow-up after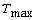 
for the solution of a semilinear heat
equation, J. Funct. Anal. 71 (1987), 142-174.
[6] T. K. Boni, On quenching of solutions for some semilinear
parabolic equations of second order, Bull. Belg. Math. Soc. 7 (2000),
73-95.
[7] T. K. Boni, Extinction for discretizations of some semilinear
parabolic equations, C. R. Acad. Sci. Paris, Sér. I 333 (2001),
795-800.
[8] C. Cortazar, M. del Pino and M. Elgueta, On the blow-up set for
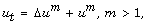Indiana Univ. Math. J. 47 (1998),
541-561.
[9] C. Cortazar, M. del Pino and M. Elgueta, Uniqueness and stability
of regional blow-up in a porous-medium equation, Ann. Inst. H.
Poincaré Anal. Non Linéaire 19 (2002), 927-960.
[10] K. Deng and H. A. Levine, On the blow-up of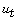 
at quenching, Proc. Amer. Math. Soc. 106
(1989), 1049-1056.
[11] K. Deng and M. Xu, Quenching for a nonlinear diffusion equation
with singular boundary condition, Z. Angew. Math. Phys. 50 (1999),
574-584.
[12] C. Fermanian Kammerer, F. Merle and H. Zaag, Stability of the
blow-up profile of nonlinear heat equations from the dynamical system
point of view, Math. Ann. 317 (2000), 195-237.
[13] M. Fila, B. Kawohl and H. A. Levine, Quenching for quasilinear
equations, Comm. Part. Diff. Equat. 17 (1992), 593-614.
[14] M. Fila and H. A. Levine, Quenching on the boundary, Nonl. Anal.
TMA 21 (1993), 795-802.
[15] A. Friedman and B. Mcleod, Blow-up of positive solutions of
nonlinear heat equations, Indiana Univ. Math. J. 34 (1985),
425-477.
[16] V. A. Galaktionov, S. P. KMiklhailov and A. A. Samarskii,
Unbounded solutions of the Cauchy problem for the parabolic equation
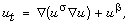Soviet Phys. Dokl. 25 (1980), 458-459.
[17] V. A. Galaktionov, Boundary value problems for the nonlinear
parabolic equation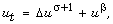 
Differ. Equat. 17 (1981), 551-555.
[18] V. Galaktionov and J. L. Vazquez, Continuation of blow-up
solutions of nonlinear heat equations in several space dimensions,
Comm. Pure Appl. Math. 50 (1997), 1-67.
[19] V. Galaktionov and J. L. Vazquez, The problem of blow-up in
nonlinear parabolic equation, current developments in PDE (Temuco,
1999), Discrete Contin. Dyn. Syst. 8 (2002), 399-433.
[20] P. Groisman, J. D. Rossi and H. Zaag, On the dependence of the
blow-up time with respect to the initial data in a semilinear
parabolic problem, Comm. Part. Diff. Equat. 28 (2003), 737-744.
[21] P. Groisman and J. D. Rossi, Dependence of the blow-up time with
respect to parameters and numerical approximations for a parabolic
problem, Asympt. Anal. 37 (2004), 79-91.
[22] J. Guo, On a quenching problem with Robin boundary condition,
Nonl. Anal. TMA 17 (1991), 803-809.
[23] M. A. Herreros and J. L. Vazquez, Generic behaviour of
one-dimensional blow up patterns, Ann. Scuola. Norm. Sup. Pisa Cl.
Sci. 19 (1992), 381-450.
[24] H. Kawarada, On solutions of initial-boundary problem for
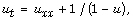Pul. Res. Inst. Math. Sci. 10 (1975),
729-736.
[25] C. M. Kirk and C. A. Roberts, A review of quenching results in
the context of nonlinear Volterra equations, Dyn. Contin. Discrete
Impuls. Syst. Ser. A Math. Anal. 10 (2003), 343-356.
[26] A. Ladyzenskaya, V. A. Solonnikov and N. N. Ural’ceva,
Linear and quasilinear equations parabolic type, Trans. Math. Monogr.,
23 AMS, Providence, RI, 1968.
[27] H. A. Levine, The quenching of solutions of linear parabolic and
hyperbolic equations with nonlinear boundary conditions, SIAM J.
Math. Anal. 14 (1983), 1139-1152.
[28] H. A. Levine, The phenomenon of quenching : A survey, in Trends
in the Theory and Practice of Nonlinear Analysis, Amsterdam,
North-Holland, (1985), 275-286.
[29] H. A. Levine, Quenching, nonquenching and beyond quenching for
solution of some parabolic equations, Ann. Math. Pure Appl. 155
(1989), 243-260.
[30] F. Merle, Solution of a nonlinear heat equation with arbitrarily
given blow-up points, Comm. Pure Appl. Math. 45 (1992), 293-300.
[31] T. Nakagawa, Blowing up on the finite difference solution to
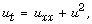Appl. Math. Optim. 2 (1976), 337-350.
[32] D. Nabongo and T. K. Boni, Quenching time for some nonlinear
parabolic equations, An. St. Univ. Ovidius Constanta 16 (2008),
87-102.
[33] D. Phillips, Existence of solution of quenching problems, Appl.
Anal. 24 (1987), 253-264.
[34] M. H. Protter and H. F. Weinberger, Maximum principles in
differential equations, Prentice Hall, Englewood Cliffs, NJ, 1967.
[35] P. Quittner, Continuity of the blow-up time and a priori bounds
for solutions in superlinear parabolic problems, Houston J. Math.
29(3) (2003), 757-799 (electronic).
[36] Q. Shang and A. Q. M. Khaliq, A compound adaptive approach to
degenerate nonlinear quenching problems, Numer. Methods Partial
Differential Equations 15 (1999), 29-47.
[37] W. Walter, Differential-und Integral-Ungleichungen, Springer,
Berlin, 1964.
