Journal of Mathematical Sciences: Advances and Applications[1] V. Adamchik and S. Wagon, A simple formula for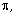 
Amer. Math. Monthly 104 (1997),
852-855.
[2] D. Anderson, The Pi-Search Page.
http://www.angio.net/pi/piquery
[3] J. Arndt and C. Haenel, Pi-Unleashed, 2nd Edition,
Springer-Verlag, Berlin, 2001.
[4] D. H. Bailey, The computation of decimal digit using
Borwein’s quartically convergent algorithm, Math. Comput. 50
(1988), 283-296.
[5] D. H. Bailey, P. B. Borwein and S. Plouffe, On the rapid
computation of various polylogarithmic constants, Math. Comput. 66
(1997), 903-913.
[6] D. H. Bailey and R. E. Crandall, On the random character of
fundamental constant expansions, Exper. Math. 10 (2001), 175-190.
http://www.nersc.gov/
dhbailey/dhbpapers/baicran.pdf
[7] D. H. Bailey, J. M. Borwein, N. J. Calkin, R. Girgensohn, D. R.
Luke and V. H. Moll, Experimental Mathematics in Action, Wellesley,
MA: A K Peters, 2007.
[8] Petr Beckmann, A History of Pi, Barnes and Noble Publishing, ISBN
0880294183, 1989.
[9] Ari. Ben-Menahem, Historical Encyclopedia of Natural and
Mathematical Sciences: Jones was first to use? for the ratio
(perimeter/diameter) of a circle, in 1706, 2009.
[10] Lennart Berggren, Jonathan M. Borwein and Peter B. Borwein
(eds.), Pi: A Source Book, Springer, 1999 (2nd Ed.), ISBN
978-0-387-98946-4.
[11] J. M. Borwein, P. B. Borwein and D. H. Bailey, Ramanujan, modular
equations, and approximations to Pi, or how to compute one billion
digits of Pi, Amer. Math. Monthly 96 (1989), 201-219.
[12] J. M. Borwein and D. H. Bailey, Mathematics by Experiment:
Plausible Reasoning in the 21st Century, Wellesley, MA: A K Peters,
2003.
[13] J. M. Borwein, Talking About Pi.
http://www.cecm.sfu.ca/personal/jborwein/picover.ht
ml
[14] C. K. Caldwell and H. Dubner, Primes in Pi, J. Recr. Math. 29
(1998), 282-289.
[15] G. W. Corder and D. I. Foreman, Nonparametric Statistics for
Non-Statisticians: A Step-by-Step Approach, Wiley, New Jersey,
2009.
[16] T. Cover and J. A. Thomas, Elements of Information Theory, Wiley,
New York, 2006.
[17] W. W. Gibbs, A digital slice of Pi, The new way to do pure math:
Experimentally, Sci. Amer. 288 (2003), 23-24.
[18] X. Gourdon and P. Sebah, PiFast: The Fastest Program to Compute
Pi.
http://numbers.computation.free.fr/Constants/PiProg
ram/pifast.html
[19] K. Gouri, R. Bhattacharyya and A. Johnson, Statistical Concepts
and Methods, John Wiley and Sons, 1977.
[20] http://www.pi314.net/eng/ramanujan.php
[21] http://numbers.computation.free.fr/Constants/Pi/pi.
html
[22] Y. Kanada, New World Record of Pi: 51.5 Billion Decimal Digits
http://www.cecm.sfu.ca/personal/jborwein/Kanada50b.
html
[23] Pi Calculated to Record Number of Digits, bbc.co.uk. 2010-01-06.
[Retrieved 2010- 01-06].
http://news.bbc.co.uk/1/hi/technology/8442255.stm
[24] Alfred S. Posamentier and Ingmar Lehmann, Pi: A Biography of the
World’s Most Mysterious Number, Prometheus Books, 2004, ISBN
978-1-59102-200-8.
[25] C. E. Shannon, A mathematical theory of communication, Bell Syst.
Tech. J. 27 (379-423) (1984), 623-656.
26] H. J. Smith, Computing Pi.
http://www.geocities.com/hjsmithh/Pi.html
[27] S. Wagon, Is normal? Math. Intel. 7 (1985), 65-67.
