Journal of Mathematical Sciences: Advances and Applications[1] Y. M. Chu and W. F. Xia, Two sharp inequalities for power mean,
geometric mean and harmonic mean, Journal of Inequalities and
Applications, Vol. 2009, Article ID 741923, 6 pages, (2009).
[2] Y. M. Chu and W. F. Xia, Inequalities for generalized logarithmic
means, Journal of Inequalities and Applications, Vol. 2009, Article ID
763252, 7 pages, (2009).
[3] Y. M. Chu and B. Y. Long, Best possible inequalities between
generalized logarithmic mean and classical means, Abstract and Applied
Analysis, Vol. 2010, Article ID 303286, 13 pages, (2010).
[4] Y. M. Chu, Y. F. Qiu, M. K. Wang and G. D. Wang, The optimal
convex combination bounds of arithmetic and harmonic means for the
Seiffert’s mean, Journal of Inequalities and Applications,
Article ID 436457, dio: 10.1155/436457, 7 pages, (2010).
[5] T. Hara, M. Uchiyama and S. E. Takahasi, A refinement of various
mean inequalities, Journal of Inequalities and Applications 2(4)
(1998), 387-395.
[6] P. A. Hästö, A monotonicity property of ratios of symmetric
homogeneous means, Journal of Inequalities in Pure and Applied
Mathematics 3(5) (2002), 1-54 (Article 71).
[7] P. A. Hästö, Optimal inequalities between Seiffert’s
mean and power mean, Mathematical Inequalities and Applications 7(1)
(2004), 47-53.
[8] A. A. Jagers, Solution of problem 887, Nieuw Archief voor Wiskunde
12 (1994), 230-231.
[9] B. Y. Long and Y. M. Chu, Optimal inequalities for generalized
logarithmic, arithmetic and geometric means, Journal of Inequalities
and Applications, Vol. 2010, Article ID 806825, 10 pages, (2010).
[10] B. Y. Long and Y. M. Chu, Optimal power mean bounds for the
weighted geometric mean of classical means, Journal of Inequalities
and Applications, Vol. 2010, Article ID 905679, 6 pages, (2010).
[11] E. Neuman and J. Sändor, On the Schwab-Borchardt mean,
Mathematica Pannonica 14(2) (2003), 253-266.
[12] E. Neuman and J. Sändor, On certain means of two arguments and
their extensions, Int. J. Math. Math. Sci. 2003(16) (2003),
981-993.
[13] E. Neuman and J. Sändor, On the Schwab-Borchardt mean,
Mathematica Pannonica 17(1) (2006), 49-59.
[14] E. Neuman and J. Sändor, Copanion inequalities for certain
bivariate means, Applicable Analysis and Discrete Mathematics 3
(2009), 46-51.
[15] H. J. Seiffert, Problem 887, Nieuw Archief voor Wiskunde 11(2)
(1993), 176.
[16] H. J. Seiffert, Ungleichungen für einen bestimmten mittelwert,
Nieuw Archief voor Wiskunde 13(2) (1995), 195-198.
[17] H. J. Seiffert, Aufgabe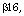 
Die Wurzel 29 (1995), 221-222.
[18] M. Y. Shi, Y. M. Chu and Y. P. Jiang, Optimal inequalities among
various means of two arguments, Abstract and Applied Analysis, Vol.
2009, Article ID 694394, 10 pages, (2009).
[19] M. K. Wang, Y. M. Chu and Y. F. Qiu, Some comparison inequalities
for generalized Muirhead and identric means, Journal of Inequalities
and Applications, Vol. 2010, Article ID 295620, 10 pages, (2010).
[20] J. J. Wen and W. L. Wang, The optimization for the inequalities
of power means, Journal of Inequalities and Applications, Vol. 2006,
Article ID 46782, 25 pages, (2006).
[21] W. F. Xia, Y. M. Chu and G. D. Wang, The optimal upper and lower
power mean bounds for a convex combination of the arithmetic and
logarithmic means, Abstract and Applied Analysis, Vol. 2010, Article
ID 604804, 9 pages, (2010).
