Journal of Mathematical Sciences: Advances and Applications[1] G. Alexopoulos, Spectral multipliers on discrete groups, Bull.
London Math. Soc. 33 (2001), 417-424.
[2] J.-Ph. Anker,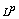 
Fourier multipliers on Riemannian symmetric
spaces of non-compact type, Ann. Math. 132 (1990), 597-628.
[3] G. Barbatis and E. Davies, Sharp bounds on heat kernels of higher
order uniformly elliptic operators, J. Oper. Theory 36 (1996),
179-198.
[4] M. Christ, 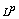bounds for spectral multipliers on
nilpotent groups, Trans. Amer. Math. Soc. 328 (1991), 73-81.
[5] R. Coifman, Analyse non-commutative sur certains espaces
homogenes, Lect. Notes in Math., Vol. 242.
[6] T. Coulhon and X. Duong, Riesz transforms for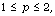 
Trans. Amer. Math. Soc. 351 (1999),
1151-1169.
[7] E. Davies, Uniformly elliptic operators with measurable
coefficients, J. Functional Anal. 132 (1995), 141-169.
[8] E. Davies, 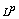spectral theory of high order elliptic
differential operators, Bull. London Math. Soc. 29 (1997), 513-546.
[9] L. De-Michele and G. Mauceri,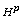 
multipliers on stratified groups, Ann. Mat.
Pura. Appl. 148 (1987), 353-366.
[10] A. F. M. T. Elst and D. W. Robinson, Weighted strongly elliptic
operators on Lie groups, J. Funct. Anal. 125 (1994), 548-603.
[11] A. F. M. T. Elst and D. W. Robinson, Elliptic operators on Lie
groups, Acta Appl. Math. 44 (1996), 133-150.
[12] A. F. M. T. Elst and D. W. Robinson, High order divergence-form
elliptic operators on Lie groups, Bull. Aust. Math. Soc. 55 (1997),
335-348.
[13] C. Feffermann, Inequalities for strongly singular convolution
operators, Acta Math. 124 (1970), 9-36.
[14] A. Georgiadis,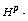 
bounds for spectral multipliers on
Riemannian manifolds, Bull. Sci. Math. 134 (2010), 750-766.
[15] A. A. Grigorýan, The heat equation on non-compact Riemannian
manifold, Mat. Sb. (182): (1) (1991), 55-87 (Russian), English
transl.: Math USSR-Sb. 72 (1992), 47-77.
[16] W. Hebisch, Multiplier theorem on generalized Heisenberg groups,
Coll. Math. 65 (1993), 231-239.
[17] L. Hörmander, Estimates for translation invariant operators in
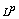spaces, Acta Math. 104 (1960), 93-139.
[18] H.-Q. Li, Estimations 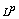des fonctions du Laplacien sur les
variétés cuspidales, Trans. Amer. Math. Soc. 357 (2004), 337-354.
[19] C.-C. Lin, Hörmander’s 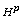multiplier theorem for the Heisenberg
group, J. London Math. Soc. 67 (2003), 686-700.
[20] S. G. Mikhlin, Multidimensional Singular Integral and Integral
Equations, Pergamon Press, Oxford, 1965.
[21] D. Müller and E. M. Stein, On spectral multipliers for
Heisenberg and related groups, J. Math. Pures Appl. 73 (1994),
413-440.
[22] I. P. Natanson, Constructive Function Theory, Vol.1, Uniform
Approximation, Frederick Unigard, N. Y., 1964.
[23] D. W. Robinson, Elliptic Operators and Lie Groups, Oxford Math.
Mon., Oxford University Press, 1991.
[24] L. Saloff-Coste, Parabolic Harnack inequality for divergence form
second order differential operators, Potential Analysis 4 (1995),
429-467.
[25] M. A. Shubin, Spectral theory of elliptic operators on
non-compact manifolds, Astérisque 207 (1992), 35-108.
[26] M. E. Taylor,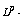 
estimates on functions of the Laplace
operator, Duke Math. Jour. 58 (1989), 773-793.
