Journal of Mathematical Sciences: Advances and Applications
DIMENSIONAL BREAKING SOLITON EQUATION[1] Y. Cheng and B. Li, Symbolic computation and construction of
soliton-like solutions to the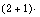 
dimensional breaking soliton equation,
Commun. Theor. Phys. (Beijing, China) 40 (2003), 137-142.
[2] R. Hirota and Y. Ohta, Hierarchies of coupled soliton equations,
I, J. Phys. Soc. Japan 60 (1991), 798-809.
[3] W. Malfliet and W. Hereman, The tanh method: I, exact solutions of
nonlinear evolution and wave equations, Phys. Scripta 54 (1996),
563-568.
[4] W. Malfliet and W. Hereman, The tanh method: II, perturbation
technique for conservative systems, Phys. Scripta 54 (1996), 569-575.
[5] Y. Z. Peng, New exact solutions for 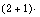dimensional breaking soliton equation,
Commun. Theor. Phys. (Beijing, China) 43 (2005), 205-207.
[6] Y. Z. Peng and E. V. Krishna, Two classes of new exact solutions
to 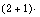dimensional breaking soliton equation,
Commun. Theor. Phys. (Beijing, China) 44 (2005), 807-809.
[7] Y. J. Ren, S. T. Liu and H. Q. Zhang, On a generalized extended
F-expansion method, Commun. Theor. Phys. (Beijing, China) 45
(2006), 15-28.
[8] F. Tascan and A. Bekir, Analytic solutions of the 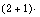dimensional nonlinear evolution equations
using the sine-cosine method, Appl. Math. 215 (2009), 3134-3139.
[9] A. M. Wazwaz, A sine-cosine method for handling nonlinear wave
equations, Math. Comput. Model. 40 (2004), 499-508.
[10] A. M. Wazwaz, A reliable treatment of the physical structure for
the nonlinear equation K(m, n), Appl. Math.
Comput. 163 (2005), 1081-1095.
[11] A. M. Wazwaz, A class of nonlinear fourth order variant of a
generalized Camassa-Holm equation with compact and noncompact
solutions, Appl. Math. Comput. 165 (2005), 485-501.
[12] S. Zhang, New exact non-travelling wave and coefficient function
solutions of the 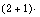dimensional breaking soliton equations, Phys.
Lett. A 368 (2007), 470-475.
