Journal of Mathematical Sciences: Advances and Applications
[1] E. Alòs, O. Mazet and D. Nualart, Stochastic calculus with
respect to Gaussian processes, Ann. Probab. 29 (2001), 766-801.
[2] E. Alòs and D. Nualart, Stochastic integration with respect to
the fractional Brownian motion, Stochastics and Stochastics Reports 75
(2003), 129-152.
[3] F. Biagini, Y. Hu, B. Øksendal and T. Zhang, Stochastic
Calculus for Fractional Brownian Motions and Applications,
Springer-Verlag, 2008.
[4] T. Bojdecki, L. G. Gorostiza and A. Talarczyk, Sub-fractional
Brownian motion and its relation to occupation times, Statist. Probab.
Lett. 69 (2004), 405-419.
[5] T. Bojdecki, L. G. Gorostiza and A. Talarczyk, Fractional Brownian
density process and its self-intersection local time of order
k, J. Theoret. Probab. 69 (2004), 717-739.
[6] T. Bojdecki, L. G. Gorostiza and A. Talarczyk, Limit theorems for
occupation time fluctuations of branching systems 1: Long-range
dependence, Stochastic Process. Appl. 116 (2006), 1-18.
[7] T. Bojdecki, L. G. Gorostiza and A. Talarczyk, Some extensions of
fractional Brownian motion and sub-fractional Brownian motion related
to particle systems, Elect. Comm. Probab. 12 (2007), 161-172.
[8] J. M. E. Guerra and D. Nualart, The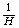 
variation of the divergence integral with
respect to the fractional Brownian motion for 
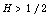and fractional Bessel processes, Stochastic
Process. Appl. 115 (2005), 91-115.
[9] Y. Hu, Integral transformations and anticipative calculus for
fractional Brownian motions, Memoirs Amer. Math. Soc. 175(825)
(2005).
[10] Y. Mishura, Stochastic calculus for fractional Brownian motions
and related processes, Lect. Notes in Math. 1929 (2008).
[11] D. Nualart, Malliavin Calculus and Related Topics, 2nd edition
Springer, New York, 2006.
[12] G. Shen and L. Yan, Remarks on sub-fractional Bessel processes,
to appear in Acta Mathematica Scientia (2010).
[13] A. V. Skorohod, On a generalization of a stochastic integral,
Theory Probab. Appl. 20 (1975), 219-233.
[14] C. Tudor, Some properties of the sub-fractional Brownian motion,
Stochastics 79 (2007), 431-448.
[15] C. Tudor, Some aspects of stochastic calculus for the
sub-fractional Brownian motion, Ann. Univ. Bucuresti, Mathematica
(2008), 199-230.
[16] C. Tudor, Inner product spaces of integrands associated to
sub-fractional Brownian motion, Statist. Probab. Lett. 78 (2008),
2201-2209.
[17] C. Tudor, On the Wiener integral with respect to a sub-fractional
Brownian motion on an interval, J. Math. Anal. Appl. 351 (2009),
456-468.
[18] L. Yan and G. Shen, On the collision local time of sub-fractional
Brownian motions, Statist. Probab. Lett. 80 (2010), 296-308.
[19] L. Yan and G. Shen, Itô formulas for the sub-fractional
Brownian motion, to appear in Commun. Stoch. Anal. (2010).
