Journal of Mathematical Sciences: Advances and Applications[1] B. Wardhaug, Encounters with Euclid, How an Ancient Greek Geometry
Text Shaped the World, Princeton University Press, 2021.
[2] B. E. Wolfinger, Simple criteria for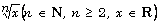 
being a rational or an irrational number,
Journal of Advances in Mathematics and Computer Science 38(9) (2023),
23-30.
DOI: https://doi.org/10.9734/jamcs/2023/v38i91801
[3] B. E. Wolfinger, Simple tests for n-th roots of natural
numbers being natural numbers and elementary methods to determine
their values, Journal of Advances in Mathematics and Computer Science
39(1) (2024), 29-35.
DOI: https://doi.org/10.9734/jamcs/2024/v39i11860
[4] C. Pomerance, Analysis and comparison of some integer
factorization algorithms, in: Discrete Algorithms and Complexity
(Editors D. S. Johnson, T. Nishizeki, A. Nozaki and H. S. Wilf),
Academic Press (1987), 119-143.
[5] D. M. Bressoud, Factorization and Primality Testing,
Springer-Verlag, 1989.
[6] M. Dietzfelbinger, Primality Testing in Polynomial time: From
Randomized Algorithms to “PRIMES is in Pâ€, Lecture Notes
in Computer Science, Volume 3000, Springer-Verlag, 2004.
DOI: https://doi.org/10.1007/b12334
