Journal of Mathematical Sciences: Advances and Applications[1] D. D. Anderson, D. F. Anderson and M. Zafrullah, Factorization in
integral domains, Journal of Pure and Applied Algebra 69(1) (1990),
1-19.
DOI: https://doi.org/10.1016/0022-4049(90)90074-R
[2] D. D. Anderson and J. R. Juett, Long length functions, Journal of
Algebra 426 (2015), 327-343.
DOI: https://doi.org/10.1016/j.jalgebra.2014.12.016
[3] S. T. Chapman, F. Gotti and M. Gotti, A survey on the atomicity of
Puiseux monoids,
Available on arXiv: https://arxiv.org/pdf/1908.09227.pdf
[4] J. Coykendall and F. Gotti, On the atomicity of monoid algebras,
arXiv: 1906.11138 [math. AC].
[5] J. Coykendall and B. Mammenga, An embedding theorem, Journal of
Algebra, 325(1) (2011), 177-185.
DOI: https://doi.org/10.1016/j.jalgebra.2010.08.026
[6] R. Gilmer, Commutative Semigroup Rings, The University of Chicago
Press, Chicago, 1984.
[7] R. Gilmer, Property E in commutative monoid rings, group and
semi-group rings (G. Karpilovsky, Editor), Elsevier Science
Publishers, B. V. (North-Holland) (1986), 13-18.
[8] R. Gipson and H. Kulosman, Atomic and AP semigroup rings
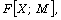where 
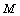is a submonoid of the additive monoid of
nonnegative rational numbers, International Electronic Journal of
Algebra 22(22) (2017), 133-146.
DOI: https://doi.org/10.24330/ieja.325939
[9] R. Gipson and H. Kulosman, For which additive submonoids
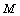of nonnegative rationals is 
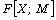AP?, preprint.
[10] F. Gotti, The elasticity of Puiseux monoids, arXiv:1703.04207
[math.AC].
[11] F. Gotti, Irreducibility and factorizations in monoid rings,
arXiv:1905.07168 [math. AC].
[12] F. Gotti, On the atomic structure of Puiseux monoids, Journal of
Algebra and its Applications 16(7) (2017); Article 1750126.
DOI: https://doi.org/10.1142/S0219498817501262
[13] I. Kaplansky, Commutative Rings, Revised Edition, The University
of Chicago Press, Chicago and London, 1974.
[14] H. Kim, Factorization in monoid domains, Communications in
Algebra 29(5) (2001), 1853-1869.
DOI: https://doi.org/10.1081/AGB-100002153
[15] H. Kulosman, A new simple example of an atomic domain which is
not ACCP, Advances in Algebra 12(1) (2019), 1-7.
[16] D. G. Northcott, Lessons on Rings, Modules and Multiplicities,
Cambridge University Press, Cambridge, 1968.
DOI: https://doi.org/10.1017/CBO9780511565922
