[1] José F. L. Aires and Marco A. S. Souto, Existence of solutions
for a quasilinear Schrödinger equation with vanishing potentials,
Journal of Mathematical Analysis and Applications 416(2) (2014),
924-946.
DOI: https://doi.org/10.1016/j.jmaa.2014.03.018
[2] José F. L. Aires and Marco A. S. Souto, Equation with positive
coefficient in the quasilinear term and vanishing potential,
Topological Methods in Nonlinear Analysis 46(2) (2015), 813-833.
DOI: https://doi.org/10.12775/TMNA.2015.069
[3] C. O. Alves and Marco A. S. Souto, Existence of solutions for a
class of nonlinear Schrödinger equations with potential vanishing
at infinity, Journal of Differential Equations 254(4) (2013),
1977-1991.
DOI: https://doi.org/10.1016/j.jde.2012.11.013
[4] C. O. Alves, Y. J. Wang and Y. T. Shen, Soliton solutions for a
class of quasilinear Schrödinger equations with a parameter,
Journal of Differential Equations 259(1) (2015), 318-343.
DOI: https://doi.org/10.1016/j.jde.2015.02.030
[5] A. Ambrosetti, V. Felli and A. Malchiodi, Ground states of
nonlinear Schrödinger equations with potentials vanishing at
infinity, Journal of the European Mathematical Society 7(1) (2005),
117-144.
DOI: https://doi.org/10.4171/JEMS/24
[6] A. Ambrosetti, A. Malchiodi and D. Ruiz, Bound states of nonlinear
Schrödinger equations with potentials vanishing at infinity,
Journal d’Analyse Mathématique 98(1) (2006), 317-348.
DOI: https://doi.org/10.1007/BF02790279
[7] A. Ambrosetti and Z. Q. Wang, Nonlinear Schrödinger equations
with vanishing and decaying potentials, Differential Integral
Equations 18(12) (2005), 1321-1332.
[8] H. Berestycki and P. L. Lions, Nonlinear scalar field equations I:
Existence of a ground state, Archive for Rational Mechanics and
Analysis 82(4) (1983), 313-345.
DOI: https://doi.org/10.1007/BF00250555
[9] L. Brizhik, A. Eremko, B. Piette and W. J. Zakrzewski, Electron
self-trapping in a discrete two-dimensional lattice, Physica D:
Nonlinear Phenomena 159(1-2) (2001), 71-90.
DOI: https://doi.org/10.1016/S0167-2789(01)00332-3
[10] D. Bonheure and J. V. Schaftingen, Groundstates for the nonlinear
Schrödinger equation with potential vanishing at infinity, Annali
di Matematica Pura ed Applicata 189(2) (2010), 273-301.
DOI: https://doi.org/10.1007/s10231-009-0109-6
[11] A. de Bouard and N. Hayashi and J. C. Saut, Global existence of
small solutions to a relativistic nonlinear Schrödinger equation,
Communications in Mathematical Physics 189(1) (1997), 73-105.
DOI: https://doi.org/10.1007/s002200050191
[12] S. T. Chen and Z. Gao, An improved result on ground state
solutions of quasilinear Schrödinger equations with super-linear
nonlinearities, Bulletin of the Australian Mathematical Society 99(2)
(2019), 231-241.
DOI: https://doi.org/10.1017/S0004972718001235
[13] B. T. Cheng and X. H. Tang, High energy solutions of modified
quasilinear fourth-order elliptic equations with sign-changing
potential, Computers & Mathematics with Applications 73(1) (2017),
27-36.
DOI: https://doi.org/10.1016/j.camwa.2016.10.015
[14] Y. K. Cheng and Y. X. Yao, Soliton solutions to a class of
relativistic nonlinear Schrödinger equations, Applied Mathematics
and Computation 260 (2015), 342-350.
DOI: https://doi.org/10.1016/j.amc.2015.03.055
[15] Y. K. Cheng and J. Yang, The existence and uniqueness result for
a relativistic nonlinear Schrödinger equation, Abstract and Applied
Analysis (2014); Article ID 362985, 1-10.
DOI: https://doi.org/10.1155/2014/362985
[16] C. M. Chu and H. D. Liu, Existence of positive solutions for a
quasilinear Schrödinger equation, Nonlinear Analysis: Real World
Applications 44 (2018), 118-127.
DOI: https://doi.org/10.1016/j.nonrwa.2018.04.007
[17] M. Colin and L. Jeanjean, Solutions for a quasilinear
Schrödinger equation: A dual approach, Nonlinear Analysis: Theory,
Methods & Applications 56(2) (2004), 213-226.
DOI: https://doi.org/10.1016/j.na.2003.09.008
[18] Y. B. Deng and W. Shuai, Non-trivial solutions for a semilinear
biharmonic problem with critical growth and potential vanishing at
infinity, Proceedings of the Royal Society of Edinburgh Section A:
Mathematics 145(2) (2015), 281-299.
DOI: https://doi.org/10.1017/S0308210513001170
[19] Y. B. Deng and W. Shuai, Positive solutions for quasilinear
Schrödinger equations with critical growth and potential vanishing
at infinity, Communications on Pure & Applied Analysis 13(6) (2014),
2273-2287.
DOI: https://doi.org/10.3934/cpaa.2014.13.2273
[20] J. M. do Ó, E. Gloss and C. Santana, Solitary waves for a
class of quasilinear Schrödinger equations involving vanishing
potentials, Advanced Nonlinear Studies 15(3) (2015), 691-714.
DOI: https://doi.org/10.1515/ans-2015-0308
[21] H. Hartmann and W. J. Zakrzewski, Electrons on hexagonal lattices
and applications to nanotubes, Physical Review B 68(18) (2003),
184-302.
DOI: https://doi.org/10.1103/PhysRevB.68.184302
[22] C. Huang and G. Jia, Existence of positive solutions for
supercritical quasilinear Schrödinger elliptic equations, Journal
of Mathematical Analysis and Applications 472(1) (2019), 705-727.
DOI: https://doi.org/10.1016/j.jmaa.2018.11.048
[23] L. Jeanjean and K. Tanaka, A positive solution for a nonlinear
Schrödinger equation on 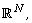 Indiana University Mathematics Journal 54(2)
(2005), 443-464.
Indiana University Mathematics Journal 54(2)
(2005), 443-464.
DOI: https://doi.org/10.1512/iumj.2005.54.2502
[24] O. Kwon, Existence of standing waves of nonlinear Schrödinger
equations with potentials vanishing at infinity, Journal of
Mathematical Analysis and Applications 387(2) (2012), 920-930.
DOI: https://doi.org/10.1016/j.jmaa.2011.09.050
[25] G. F. Li, Y. S Huang and Z. Liu, Positive solutions for
quasilinear Schrödinger equations with superlinear term, Complex
Variables and Elliptic Equations 65(6) (2019), 936-955.
DOI: https://doi.org/10.1080/17476933.2019.1636791
[26] G. F. Li and Y. S Huang, Positive solutions for generalized
quasilinear Schrödinger equations with asymptotically linear
nonlinearities, Applicable Analysis (2019).
DOI: https://doi.org/10.1080/00036811.2019.1634256
[27] J. Q. Liu, Y. Q. Wang and Z. Q. Wang, Solutions for quasilinear
Schrödinger equations via the Nehari method, Communications in
Partial Differential Equations 29(5-6) (2004), 879-901.
DOI: https://doi.org/10.1081/PDE-120037335
[28] Z. P. Liang, J. F. Gao and A. R. Li, Infinitely many solutions to
a quasilinear Schrödinger equation with a local sublinear term,
Applied Mathematics Letters 89 (2019), 22-27.
DOI: https://doi.org/10.1016/j.aml.2018.09.015
[29] Q. Q. Li, K. M. Teng and X. Wu, Existence of positive solutions
for a class of critical fractional Schrödinger equations with
potential vanishing at infinity, Mediterranean Journal of Mathematics
14(2) (2017); Article 80.
DOI: https://doi.org/10.1007/s00009-017-0846-5
[30] Q. Q. Li and X. Wu, Existence, multiplicity, and concentration of
solutions for generalized quasilinear Schrödinger equations with
critical growth, Journal of Mathematical Physics 58(4) (2017); Article
041501.
DOI: https://doi.org/10.1063/1.4982035
[31] Q. Q. Li and X. Wu, Multiple solutions for generalized
quasilinear Schrödinger equations, Mathematical Methods in the
Applied Sciences 40(5) (2017), 1359-1366.
DOI: https://doi.org/10.1002/mma.4050
[32a] P. L. Lions, The concentration-compactness principle in the
calculus of variation, The locally compact case: Part I, Annales de
l’I.H.P: Analyse Non Linéaire 1(2) (1984), 109-145.
[32b] P. L. Lions, The concentration-compactness principle in the
calculus of variation, The locally compact case: Part II, Annales de
l’I.H.P: Analyse Non Linéaire 1(4) (1984), 223-283.
[33] X. Q. Liu, J. Q. Liu and Z. Q. Wang, Quasilinear elliptic
equations via perturbation method, Proceedings of the American
Mathematical Society 141(1) (2013), 253-263.
DOI: https://doi.org/10.1090/S0002-9939-2012-11293-6
[34] J. Q. Liu, X. Q. Liu and Z. Q. Wang, Multiple sign-changing
solutions for quasilinear elliptic equations via perturbation method,
Communications in Partial Differential Equations 39(12) (2014),
2216-2239.
DOI: https://doi.org/10.1080/03605302.2014.942738
[35] X. Q. Liu, J. Q. Liu and Z. Q. Wang, Quasilinear elliptic
equations with critical growth via perturbation method, Journal of
Differential Equations 254(1) (2013), 102-124.
DOI: https://doi.org/10.1016/j.jde.2012.09.006
[36] X. N. Liu and H. B. Chen, Positive solutions for a class of
quasilinear Schrödinger equations with vanishing potentials,
Boundary Value Problems (2017); Article ID 35, 11 pages.
DOI: https://doi.org/10.1186/s13661-017-0769-x
[37] V. F. Morales Delgado, J. F. Gómez Aguilar and D. Baleanu, A
new approach to exact optical soliton solutions for the nonlinear
Schrödinger equation, European Physical Journal Plus 133(5) (2018);
Article ID 189.
DOI: https://doi.org/10.1140/epjp/i2018-12020-4
[38] M. Poppenberg, K. Schmitt and Z. Q. Wang, On the existence of
soliton solutions to quasilinear Schrödinger equations, Calculus of
Variations and Partial Differential Equations 14(3) (2002),
329-344.
DOI: https://doi.org/10.1007/s005260100105
[39] P. H. Rabinowitz, in: Minimax Methods in Critical Point Theory
with Applications to Differential Equations, in: CBMS Regional
Conference Series in Mathematics, Volume 65, American Mathematical
Society, Providence RI, 1986.
[40] D. Ruiz and G. Siciliano, Existence of ground states for a
modified nonlinear Schrödinger equation, Nonlinearity 23(5) (2010),
1221-1233.
DOI: https://doi.org/10.1088/0951-7715/23/5/011
[41] U. B. Severo, E. Gloss and E. D. da Silva, On a class of
quasilinear Schrödinger equations with superlinear or
asymptotically linear terms, Journal of Differential Equations 263(6)
(2017), 3550-3580.
DOI: https://doi.org/10.1016/j.jde.2017.04.040
[42] U. B. Severo and M. Gilson de Carvalho, Quasilinear
Schrödinger equations with unbounded or decaying potentials,
Mathematische Nachrichten 291(2-3) (2018), 492-517.
DOI: https://doi.org/10.1002/mana.201600028
[43] U. B. Severo and G. M. de Carvalho, Quasilinear Schrödinger
equations with a positive parameter and involving unbounded or
decaying potentials, Applicable Analysis (2019).
DOI: https://doi.org/10.1080/00036811.2019.1599106
[44] Y. T. Shen and Y. J. Wang, Standing waves for a class of
quasilinear Schrödinger equations, Complex Variables and Elliptic
Equations 61(6) (2016), 817-842.
DOI: https://doi.org/10.1080/17476933.2015.1119818
[45] Y. T. Shen and Y. J. Wang, Soliton solutions for generalized
quasilinear Schrödinger equations, Nonlinear Analysis: Theory,
Methods & Applications 80 (2013), 194-201.
DOI: https://doi.org/10.1016/j.na.2012.10.005
[46] Y. T. Shen and Y. J. Wang, Standing waves for a relativistic
quasilinear asymptotically Schrödinger equation, Applicable
Analysis 95(11) (2016), 2553-2564.
DOI: https://doi.org/10.1080/00036811.2015.1100296
[47] Y. T. Shen and Y. J. Wang, A class of generalized quasilinear
Schrödinger equations, Communications on Pure & Applied Analysis
15(3) (2016), 853-870.
DOI: https://doi.org/10.3934/cpaa.2016.15.853
[48] H. X. Shi and H. B. Chen, Positive solutions for generalized
quasilinear Schrödinger equations with potential vanishing at
infinity, Applied Mathematics Letters 61 (2016), 137-142.
DOI: https://doi.org/10.1016/j.aml.2016.06.004
[49] H. X. Shi and H. B. Chen, Existence and multiplicity of solutions
for a class of generalized quasilinear Schrödinger equations,
Journal of Mathematical Analysis and Applications 452(1) (2017),
578-594.
DOI: https://doi.org/10.1016/j.jmaa.2017.03.020
[50] H. X. Shi and H. B. Chen, Infinitely many solutions for
generalized quasilinear Schrödinger equations with a finite
potential well, Bulletin of the Iranian Mathematical Society 44(3)
(2018), 691-705.
DOI: https://doi.org/10.1007/s41980-018-0044-7
[51] Elves A. B. Silva and Gilberto F. Vieira, Quasilinear
asymptotically periodic Schrödinger equations with critical growth,
Calculus of Variations and Partial Differential Equations 39(1)
(2010), 1-33.
DOI: https://doi.org/10.1007/s00526-009-0299-1
[52] Y. J. Wang, Solitary solutions for a class of Schrödinger
equations in 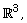 Zeitschrift für angewandte Mathematik und
Physik 67(4) (2016); Article ID 88, 17 pages.
Zeitschrift für angewandte Mathematik und
Physik 67(4) (2016); Article ID 88, 17 pages.
DOI: https://doi.org/10.1007/s00033-016-0679-2
[53] Y. J. Wang, A class of quasilinear Schrödinger equations with
critical or supercritical exponents, Computers & Mathematics with
Applications 70(4) (2015), 562-572.
DOI: https://doi.org/10.1016/j.camwa.2015.05.016
[54] X. Y. Yang, W. B. Wang and F. K. Zhao, Infinitely many radial and
non-radial solutions to a quasilinear Schrödinger equation,
Nonlinear Analysis: Theory, Methods & Applications 114 (2015),
158-168.
DOI: https://doi.org/10.1016/j.na.2014.11.015
[55] Z. P. Yang and F. K. Zhao, Three solutions for a fractional
Schrödinger equation with vanishing potentials, Applied Mathematics
Letters 76 (2018), 90-95.
DOI: https://doi.org/10.1016/j.aml.2017.08.004
[56] W. Zhang, J. Zhang and Z. M. Luo, Multiple solutions for the
fourth-order elliptic equation with vanishing potential, Applied
Mathematics Letters 73 (2017), 98-105.
DOI: https://doi.org/10.1016/j.aml.2017.04.030