Journal of Mathematical Sciences: Advances and Applications
POWER OF STOKES OPERATOR[1] P. Moon and D. E. Spencer, Field Theory Handbook, Springer-Verlag,
1961.
[2] P. M. Morse and H. Feshbach, Methods of Theoretical Physics,
McGraw-Hill, 1953.
[3] R. P. Eisenhart, Separable systems of Stackel, Annals of
Mathematics 35(2) (1934), 284-305.
DOI: https://doi.org/10.2307/1968433
[4] P. Moon and D. E. Spencer, Separability conditions for the Laplace
and Helmholtz equations, Journal of the Franklin Institute 253(6)
(1952), 585-600.
DOI: https://doi.org/10.1016/0016-0032(52)90682-0
[5] P. Moon and D. E. Spencer, Separability in a class of coordinate
systems, Journal of the Franklin Institute 254(3) (1952), 227-242.
DOI: https://doi.org/10.1016/0016-0032(52)90460-2
[6] P. Moon and D. E. Spencer, Some coordinate systems associated with
elliptic functions, Journal of the Franklin Institute 255(6) (1953),
531-543.
DOI: https://doi.org/10.1016/0016-0032(53)90302-0
[7] P. Moon and D. E. Spencer, Theorems on separability in Riemannian
n-space, Proceedings of the American Mathematical Society 3(4)
(1952), 635-642.
DOI: https://doi.org/10.1090/S0002-9939-1952-0049439-7
[8] P. Moon and D. E. Spencer, Recent investigations of the separation
of Laplace’s equation, Proceedings of the American Mathematical
Society 4(2) (1953), 302-307.
DOI: https://doi.org/10.1090/S0002-9939-1953-0053335-X
[9] E. Almansi, Sull’integrazione dell’equazione
differenziale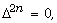 
Annali di Matematica Pura ed Applicata 2(1)
(1899), 1-51.
DOI: https://doi.org/10.1007/BF02419286
[10] J. Happel and H. Brenner, Low Reynolds Number Hydrodynamics,
Kluwer Academic Publishers, Dordrecht, The Netherlands, 1991.
[11] E. Protopapas, On the solution of irrotational Stokes flow in
rotational system of coordinates, Submitted for publication.
[12] G. Dassios, M. Hadjinicolaou and A. C. Payatakes, Generalized
eigenfunctions and complete semiseparable solutions for Stokes flow in
spheroidal coordinates, Quarterly of Applied Mathematics 52(1) (1994),
157-191.
DOI: https://doi.org/10.1090/qam/1262325
[13] M. Hadjinicolaou and E. Protopapas, On the R-semiseparation of
the Stokes bi-stream operator in inverted prolate spheroidal geometry,
Mathematical Methods in the Applied Sciences 37(2) (2014), 207-211.
DOI: https://doi.org/10.1002/mma.2841
[14] M. Hadjinicolaou and E. Protopapas, Spectral decomposition of the
Stokes flow operators in the inverted prolate spheroidal coordinates,
IMA Journal of Applied Mathematics 80(5) (2015), 1475-1491.
DOI: https://doi.org/10.1093/imamat/hxv003
[15] M. Hadjinicolaou and E. Protopapas, Eigenfunction expansions for
the Stokes flow operators in the inverted oblate coordinate system,
Mathematical Problems in Engineering (2016); Article ID 9049131.
DOI: http://dx.doi.org/10.1155/2016/9049131
[16] S. Deo and A. Tiwari, On the solution of a partial differential
equation representing irrotational flow in bispherical polar
coordinates, Applied Mathematics and Computation 205(1) (2008),
475-477.
DOI: https://doi.org/10.1016/j.amc.2008.08.023
[17] M. Hadjinicolaou and E. Protopapas, Necessary and sufficient
conditions for the separability and the R-separability of the
irrotational Stokes equation, Submitted for publication.
[18] A. Charalambopoulos and G. Dassios, Complete decomposition of
axisymmetric Stokes flow, International Journal of Engineering Science
40(10) (2002), 1099-1111.
DOI: https://doi.org/10.1016/S0020-7225(02)00004-6
[19] G. Dassios and P. Vafeas, On the spheroidal semiseparation for
Stokes flow (2008); Article ID 135289.
DOI: https://doi.org/10.1155/2008/135289
[20] N. N. Lebedev, Special Functions and their Applications, Dover
Publications, 1972.
