Journal of Mathematical Sciences: Advances and Applications
[1] Andras Batkai, Marjeta Kramar Fijavz and Abdelaziz Rhandi,
Positive Operator Semigroups, Birkhauser, 2017.
[2] Y. Giga and T. Miyakava, Solutions in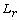 
of the Navier-Stokes initial value problem,
Archive for Rational Mechanics and Analysis 89(3) (1985), 267-281.
DOI: https://doi.org/10.1007/BF00276875
[3] H. Fujita and T. Kato, On the Navier-Stokes initial value problem:
I, Archive for Rational Mechanics and Analysis 16(4) (1964),
269-315.
DOI: https://doi.org/10.1007/BF00276188
[4] T. Kato, Strong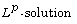 
of the Navier-Stokes equation in 
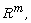with application to weak solutions,
Mathematische Zeitschrift 187(4) (1984), 471-480.
DOI: https://doi.org/10.1007/BF01174182
[5] Klaus-Jochen Engel and Rainer Nagel, One-Parameter Semigroups for
Linear Evolution Equations, Springer, 2000.
[6] E. Kreyszig, Introduction Functional Analysis with Applications,
John Wiley & Sons, 1978.
[7] Peter Meyer-Nieberg, Banach Lattices, Springer-Verlag, 1991.
[8] M. Otelbaev, Existence of a strong solution of the Navier-Stokes
equation, Mathematical Journal (ISSN 1682-0525) 13(4) (2013),
5-104.
[9] James C. Robinson, Infinite-Dimensional Dynamical Systems,
Cambridge University Press, 2001.
[10] Veli B. Shakhmurov, Nonlocal Navier-Stokes problems in abstract
function spaces and applications, Nonlinear Analysis: Real World
Applications 26 (2015), 19-43.
DOI: https://doi.org/10.1016/j.nonrwa.2015.03.011
[11] A. Pazy, Semigroups of Linear Operators and Applications to
Partial Differential Equations, Springer Verlag (1983, reprint in
China in 2006).
[12] K. Yosida, Functional Analysis, 6th Edition, Springer Verlag,
1980.
