Journal of Mathematical Sciences: Advances and Applications[1] A. Abolarinwa and T. Apata,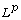 
-Hardy-Rellich and uncertainty principle
inequalities on the sphere, Advances in Operator Theory 3(4) (2018),
745-762.
DOI: https://doi.org/10.15352/aot.1712-1282
[2] P. Baras and J. A. Goldstein, The heat equation with a singular
potential, Transactions of the American Mathematical Society 284(1)
(1984), 121-139.
DOI: https://doi.org/10.1090/S0002-9947-1984-0742415-3
[3] H. Brezis and J. L. Vázquez, Blow-up solutions of some
nonlinear elliptic problems, Revista Matemática de la Universidad
Complutense de Madrid 10(2) (1997), 443-469.
[4] G. Carron, Inégalités de Hardy sur les variétés
Riemanniennes non-compactes, Journal de Mathématiques Pures et
Appliquées 76(10) (1997), 883-891.
DOI: https://doi.org/10.1016/S0021-7824(97)89976-X
[5] F. Dai and Y. Xu, The Hardy-Rellich inequality and uncertainty
principle on the sphere, Constructive Approximation 40(1) (2014),
141-171.
DOI: https://doi.org/10.1007/s00365-014-9235-5
[6] Y. Di, L. Jiang, S. Shen and Y. Jin, A note on a class of
Hardy-Rellich type inequalities, Journal of Inequalities and
Applications (2013); Article 84.
DOI: https://doi.org/10.1186/1029-242X-2013-84
[7] F. Du and J. Mao, Hardy and Rellich type inequalities on metric
measure spaces, Journal of Mathematical Analysis and Applications
429(1) (2015), 354-365.
DOI: https://doi.org/10.1016/j.jmaa.2015.04.021
[8] L. D’Ambrosio and S. Dipierro, Hardy inequalities on
Riemannian manifolds and applications, Annales de l'Institut Henri
Poincare (C) Non Linear Analysis 31(3) (2014), 449-475.
DOI: https://doi.org/10.1016/j.anihpc.2013.04.004
[9] G. Grillo, Hardy and Rellich-type inequalities for metrics defined
by vector fields, Potential Analysis 18(3) (2003), 187-217.
DOI: https://doi.org/10.1023/A:1020963702912
[10] J. P. Garcia Azorero and I. P. Alonso, Hardy inequalities and
some critical elliptic and parabolic problems, Journal of Differential
Equations 144(2) (1998), 441-476.
DOI: https://doi.org/10.1006/jdeq.1997.3375
[11] I. Kombe, The linear heat equation with highly oscillating
potential, Proceedings of the American Mathematical Society 132(9)
(2004), 2683-2691.
DOI: https://doi.org/10.1090/S0002-9939-04-07392-7
[12] I. Kombe and M. Özaydin, Improved Hardy and Rellich
inequalities on Riemannian manifolds, Transactions of the American
Mathematical Society 361(12) (2009), 6191-6203.
DOI: https://doi.org/10.1090/S0002-9947-09-04642-X
[13] X. Sun and F. Pan, Hardy type inequalities on the sphere, Journal
of Inequalities and Applications (2017); Article 148.
DOI: https://doi.org/10.1186/s13660-017-1424-x
[14] J. L. Vázquez and E. Zuazua, The Hardy inequality and the
asymptotic behaviour of the heat equation with an inverse-square
potential, Journal of Functional Analysis 173(1) (2000), 103-153.
DOI: https://doi.org/10.1006/jfan.1999.3556
[15] Y. Xiao, Some Hardy inequalities on the sphere, Journal of
Mathematical Inequalities 10(3) (2016), 793-805.
DOI: https://doi.org/10.7153/jmi-10-64
[16] Q. Yang, D. Su and Y. Kong, Hardy inequalities on Riemannian
manifolds with negative curvature, Communications in Contemporary
Mathematics 16(2) (2014); Article 1350043, 24 pages.
DOI: https://doi.org/10.1142/S0219199713500430
[17] S. Yin, A sharp Hardy type inequality on the sphere, New York
Journal of Mathematics 24 (2018), 1101-1110.
[18] S. Yin, A sharp Rellich inequality on the sphere, Mathematics
6(12) (2018); Article 288.
DOI: https://doi.org/10.3390/math6120288
