[1] R. Alexandre, Homogenisation and 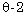 convergence, Proceedings of the Royal Society
of Edinburgh Section A: Mathematics 127(3) (1997), 441-455.
convergence, Proceedings of the Royal Society
of Edinburgh Section A: Mathematics 127(3) (1997), 441-455.
DOI: https://doi.org/10.1017/S0308210500029863
[2] G. Allaire, Homogenization of the Unsteady Stokes Equations in
Porous Media, Progress in Partial Differential Equations: Calculus of
Variations, Applications, Pont-Ã -Mousson, 1991.
[3] G. Allaire, Homogenization and two-scale convergence, SIAM Journal
on Mathematical Analysis 23(6) (1992), 1482-1518.
DOI: https://doi.org/10.1137/0523084
[4] G. Allaire, Two-Scale Convergence and Homogenization of Periodic
Structures, 1993.
[5] G. Allaire, Introduction to Homogenization Theory, VKI Lecture
Series 2001-2002 Multiscale Methods, Lecture 1, 2002.
[6] G. Allaire and M. Briane, Multiscale convergence and reiterated
homogenisation, Proceedings of the Royal Society of Edinburgh Section
A: Mathematics 126(2) (1996), 297-342.
DOI: https://doi.org/10.1017/S0308210500022757
[7] G. Allaire and C. Conca, Boundary layers in the homogenization of
a spectral problem in fluid-solid structures, SIAM Journal on
Mathematical Analysis 29(2) (1998), 343-379.
DOI: https://doi.org/10.1137/S0036141096304328
[8] G. Allaire, A. Damlamian and U. Hornung, Two-scale convergence on
periodic surfaces and applications, In Proceedings of the
International Conference on Mathematical Modelling of Flow Through
Porous Media (May 1995), A. Bourgeat et al., Editors, (1996),
15-25.
[9] G. Allaire and K. El Ganaoui, Homogenization of a conductive and
radiative heat transfer problem, Multiscale Modeling & Simulation 7(3)
(2008), 1148-1170.
DOI: https://doi.org/10.1137/080714737
[10] F. Alouges, Introduction to Periodic Homogenization, Minicourse
in Tohoku University 4 (2016).
http://www.cmap.polytechnique.fr/~alouges/Homogenization/CoursHomog.pd
f
[11] M. Amar, Two-scale convergence and homogenization on BV(Ω),
Asymptotic Analysis 16(1) (1998), 65-84.
[12] S. N. Antontsev, A. M. Meirmanov and V. V. Yurinsky,
Homogenization of stokes-type equations with variable viscosity,
Siberian Advances in Mathematics 8(2) (1998), 1-29.
[13] T. Arbogast, J. Douglas and U. Hornung, Derivation of the double
porosity model of single phase flow via homogenization theory, SIAM
Journal on Mathematical Analysis 21(4) (1990), 823-836.
DOI: https://doi.org/10.1137/0521046
[14] I. Babuska, Solution of problems with interfaces and
singularities, In Symposium on Mathematical Aspects of Finite Elements
in Partial Differential Equations Academic Press, New York (1974),
pages 213-277.
DOI: https://doi.org/10.1016/B978-0-12-208350-1.50013-3
[15] I. Babuska, Homogenization approach in engineering, Computing
Methods in Applied Sciences and Engineering (1975), 137-153.
DOI: https://doi.org/10.1007/978-3-642-85972-4_8
[16a] I. Babuska, Solution of interface problems by homogenization: I,
SIAM Journal on Mathematical Analysis 7(5) (1976), 603-634.
DOI: https://doi.org/10.1137/0507048
[16b] I. Babuska, Solution of interface problems by homogenization:
II, SIAM Journal on Mathematical Analysis 7(5) (1976), 635-645.
DOI: https://doi.org/10.1137/0507049
[16c] I. Babuska, Solution of interface problems by homogenization:
III, SIAM Journal on Mathematical Analysis 8(6) (1977), 923-937.
DOI: https://doi.org/10.1137/0508071
[17] A. Back and E. Frenod, Geometric two-scale convergence on
manifold and applications to the vlasov equation, Discrete and
Continuous Dynamical Systems - Series S 8(1) (2015), 223-241.
DOI: https://doi.org/10.3934/dcdss.2015.8.223
[18] N. Bakhvalov and G. Panasenko, Homogenisation: Averaging
Processes in Periodic Media, Kluwer, Dordrecht, 1989.
[19] A. Bensoussan, J. L. Lions and G. Papanicolaou, Asymptotic
Analysis for Periodic Structures, Volume 5 of Studies in Mathematics
and its Applications, North-Holland Publishing Co., Amsterdam,
1978.
[20] W. Bielski, J. J. Telega and R. Wojnar, Nonstationary flow of a
viscous fluid through a porous elastic medium: Asymptotic analysis and
two-scale convergence, Mechanics Research Communications 26(5) (1999),
619-628.
DOI: https://doi.org/10.1016/S0093-6413(99)00070-1
[21] A. Bourgeat and A. Hidanl, Effective model of two-phase flow in a
porous medium made of different rock types, Applicable Analysis
58(1-2) (1995), 1-29.
DOI: https://doi.org/10.1080/00036819508840360
[22] A. Bourgeat, S. Luckhaus and A. Mikelic, Convergence of the
homogenization process for a double-porosity model of immiscible
two-phase flow, SIAM Journal on Mathematical Analysis 27(6) (1996),
1520-1543.
DOI: https://doi.org/10.1137/S0036141094276457
[23] S. Wright, A. Mikelic and A. Bourgeat, Stochastic two-scale
convergence in the mean and applications, Journal für die Reine und
Angewandte Mathematik 456 (1994), 19-51.
DOI: https://doi.org/10.1515/crll.1994.456.19
[24] D. Caillerie, Homogénéisation des matériaux Ã
structure périodique, Méthodes Asymptotiques en Mécanique.
http://mam.ida.upmc.fr/Telechargements/cours-Caillerie.pdf
[25] É. Canon and J. N. Pernin, Homogenization of Diffusion in a
Composite Medium with Interfacial Barrier, Comptes Rendus de
l’Académie des Sciences, Series I: Mathematics 325(1)
(1997), 123-126.
DOI: https://doi.org/10.1016/S0764-4442(97)83946-8
[26] J. Casado-Diaz and I. Gayte, A general compactness result and its
application to the two-scale convergence of almost periodic functions,
Comptes Rendus de l’Académie des Sciences, Series I:
Mathematics 323(4) (1996), 329-334.
[27] P. Cazeaux and C. Grandmont, Homogenization of a multiscale
viscoelastic model with nonlocal damping, application to the human
lungs, Mathematical Models and Methods in Applied Sciences 25(6)
(2015), 1125-1177.
DOI: https://doi.org/10.1142/S0218202515500293
[28] R. M. Christensen, Mechanics of Composite Materials, John Wiley,
New-York, 1979.
[29] D. Cioranescu, A. Damlamian and G. Griso, Periodic unfolding and
homogenization, Comptes Rendus Mathematique 335(1) (2002), 99-104.
DOI: https://doi.org/10.1016/S1631-073X(02)02429-9
[30] D. Cioranescu, A. Damlamian and G. Griso, The periodic unfolding
method in homogenization, SIAM Journal on Mathematical Analysis 40(4)
(2008), 1585-1620.
DOI: https://doi.org/10.1137/080713148
[31] D. Cioranescu and P. Donato, An Introduction to Homogenization,
Oxford, 1999.
[32] G. W. Clark and L. A. Packer, Two-scale homogenization of
implicit degenerate evolution equations, Journal of Mathematical
Analysis and Applications 214(2) (1997), 420-438.
DOI: https://doi.org/10.1006/jmaa.1997.5577
[33] G. W. Clark and L. A. Packer, Two-scale homogenization of
non-linear degenerate evolution equations, Journal of Mathematical
Analysis and Applications 238(1) (1999), 316-328.
DOI: https://doi.org/10.1006/jmaa.1999.6547
[34] G. W. Clark and R. E. Showalter, Two-scale convergence of a model
for flow in a partially fissured medium, Electronic Journal of
Differential Equations (1999), 1-20; Article 2.
[35] C. Conca, J. Planchard and M. Vanninathan, Fluids and Periodic
Structures, RAM: Research in Applied Mathematics, 1995.
[36] D. Cioranescu, P. Donato and R. Zaki, Periodic unfolding and
robin problems in perforated domains, Comptes Rendus Mathematique
342(7) (2006), 469-474.
DOI: https://doi.org/10.1016/j.crma.2006.01.028
[37] A. Ene and J. Saint Jean Paulin, On a model of fractured porous
media, Mathematical Modelling of Flow Through Porous Media (1995),
pages 402-409.
[38] I. A. Ene and J. Saint Paulin, Homogenization and two-scale
convergence for a Stokes or Navier-Stokes flow in an elastic thin
porous medium, Mathematical Models and Methods in Applied Sciences
6(7) (1996), 941-955.
DOI: https://doi.org/10.1142/S0218202596000389
[39] Jan Francu, On two-scale convergence and periodic unfolding,
Tatra Mountains Mathematical Publications 48(1) (2011), 73-81.
DOI: https://doi.org/10.2478/v10127-011-0007-3
[40] E. Frénod and E. Sonnendrucker, Long time behavior of the
two-dimensional Vlasov equation with a strong external magnetic field,
Mathematical Models and Methods in Applied Sciences 10(4) (2000),
539-553.
DOI: https://doi.org/10.1142/S021820250000029X
[41] Z. Habibi, Homogenization and Two Scales Convergence of Some
Stationary and Non-stationary Heat Transfer Problems, Application to
Gas Cooled Nuclear Rectors, PhD Thesis, École Polytechnique,
Paris, 2011.
[42] Z. Hashin, The elastic moduli of heterogeneous materials, Journal
of Applied Mechanics 29(1) (1962), 143-150.
DOI: https://doi.org/10.1115/1.3636446
[43] Z. Hashin, Analysis of composite materials: A survey, Journal of
Applied Mechanics 50(3) (1983), 481-505.
DOI: https://doi.org/10.1115/1.3167081
[44] A. Holmbom, Homogenization of parabolic equations an alternative
approach and some corrector-type results, Applications of Mathematics
42(5) (1997), 321-343.
DOI: https://doi.org/10.1023/A:1023049608047
[45] U. Hornung, Homogenization and Porous Media, Springer Verlag,
1997.
[46] J. Jiang and C. Lin, Weak turbulence plasma induced by two-scale
homogenization, Journal of Mathematical Analysis and Applications
410(2) (2014), 585-596.
DOI: https://doi.org/10.1016/j.jmaa.2013.08.010
[47] S. Kesavan, Homogenization of elliptic eigenvalue problems: Part
2, Applied Mathematics and Optimization 5(1) (1979), 197-216.
DOI: https://doi.org/10.1007/BF01442554
[48] R. Lipton and B. Vernescu, Homogenisation of two-phase emulsions,
Proceedings of the Royal Society of Edinburgh Section A: Mathematics
124(6) (1994), 1119-1134.
DOI: https://doi.org/10.1017/S0308210500030146
[49] D. Lukkassen, G. Nguetseng and P. Wall, Two-scale convergence,
International Journal of Pure and Applied Mathematics 2(1) (2002),
35-86.
[50] R. E. Miller, Homogenization of time-dependent systems with
Kelvin-Voigt damping by two-scale convergence, Discrete & Continuous
Dynamical Systems: A 1(4) (1995), 485-502.
DOI: https://doi.org/10.3934/dcds.1995.1.485
[51] A. K. Nandakumaran and S. Sivaji Ganesh, Lectures on two scale
convergence and homogenization, In NPDE-TCA Advanced Workshop on
Homogenization, Control Theory and Applications, 2016.
[52] A. K. Nandakumaran and M. Rajesh, Homogenization of a nonlinear
degenerate parabolic differential equation, Electronic Journal of
Differential Equations (2001), 1-19; Article 17.
[53] L. Nechvátal, Alternative approaches to the two-scale
convergence, Applications of Mathematics 49(2) (2004), 97-110.
DOI: https://doi.org/10.1023/B:APOM.0000027218.04167.9b
[54] M. Neuss-Radu, Some extensions of two-scale convergence, Comptes
Rendus de l'Académie des Sciences, Series I: Mathematics 322(9)
(1996), 899-904.
[55] G. Nguetseng, A general convergence result for a functional
related to the theory of homogenization, SIAM Journal on Mathematical
Analysis 20(3) (1989), 608-623.
DOI: https://doi.org/10.1137/0520043
[56] G. Nguetseng, Homogenization structures and applications I,
Zeitschrift für Analysis und Ihre Anwendungen 22(1) (2003),
73-107.
DOI: https://doi.org/10.4171/zaa/1133
[57] G. Nguetseng, Homogenization structures and applications II,
Zeitschrift für Analysis und Ihre Anwendungen 23(3) (2004),
483-508.
DOI: https://doi.org/10.4171/zaa/1208
[58] G. Nguetseng and N. Svanstedt, 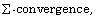 Banach Journal of Mathematical Analysis 5(1)
(2011), 101-135.
Banach Journal of Mathematical Analysis 5(1)
(2011), 101-135.
[59] R. P. Gilbert and A. Mikelic, Homogenizing the acoustic
properties of the seabed: Part 1, Nonlinear Analysis: Theory, Methods
& Applications 40(1-8) (2000), 185-212.
DOI: https://doi.org/10.1016/S0362-546X(00)85011-7
[60] D. Polisevski and J. Saint Jean-Paulin, Homogenization of
stokes-Boussinesq flows in a quasiperiodic domain, Revue Roumaine de
Mathématique Pures et Appliquées 40(9-10) (1995), 797-808.
[61] M. L. Mascarenhas and D. Polisevski, The warping, the torsion and
the Neumann problems in a quasi-periodically perforated domain,
Mathematical Modelling and Numerical Analysis 28(1) (1994), 37-57.
DOI: https://doi.org/10.1051/m2an/1994280100371
[62] M. Rajesh, Correctors for flow in a partially fissured medium,
Electronic Journal of Differential Equations (1999), 1-15; Article
27.
[63] E. Sanchez-Palencia, Non-Homogeneous Media and Vibration Theory,
Springer, 1980.
[64] N. Wellander, Homogenization of the Maxwell equations: Case I,
linear theory, Applications of Mathematics 46(1) (2001), 29-51.
DOI: https://doi.org/10.1023/A:1013727504393
[65] X. Zhang, Two-scale convergence and homogenization for a class of
quasilinear elliptic equations, Journal of Partial Differential
Equations 9(3) (1996), 263-276.