[1] F. S. Khodadad, F. Nazari, M. Eslami and H. Rezazadeh, Soliton
solutions of the conformable fractional Zakharov-Kuznetsov equation
with dual-power law nonlinearity, Optical and Quantum Electronics
49(11) (2017); Article 384, 12 pages.
DOI: https://doi.org/10.1007/s11082-017-1225-y
[2] M. Eslami, H. Rezazadeh, M. Rezazadeh and S. S. Mosavi, Exact
solutions to the space-time fractional Schrödinger-Hirota equation
and the space-time modified KdV-Zakharov-Kuznetsov equation, Optical
and Quantum Electronics 49(8) (2017); Article 279, 15 pages.
DOI: https://doi.org/10.1007/s11082-017-1112-6
[3] S. Sahoo and S. S. Ray, Analysis of Lie symmetries with
conservation laws for the (3+1) dimensional time-fractional mKdV-ZK
equation in ion-acoustic waves, Nonlinear Dynamic 90(2) (2017),
1105-1113.
DOI: https://doi.org/10.1007/s11071-017-3712-x
[4] Y. Cenesiz, O. Tasbozan and A. Kurt, Functional variable method
for conformable fractional modified KdV-ZK equation and Maccari
system, Tbilisi Mathematical Journal 10(1) (2017), 117-125.
[5] S. Sahoo and S. S. Ray, Improved fractional sub-equation method
for (3+1)-dimensional generalized fractional KdV-Zakharov-Kuznetsov
equations, Computers and Mathematics with Applications 70(2) (2015),
158-166.
DOI: https://doi.org/10.1016/j.camwa.2015.05.002
[6] M. T. Islam, M. A. Akbar and M. A. K. Azad, Closed-form travelling
wave solutions to the nonlinear space-time fractional coupled
Burgers’ equation, Arab Journal of Basic and Applied Sciences
26(1) (2019), 1-11.
DOI: https://doi.org/10.1080/25765299.2018.1523702
[7] W. Malfliet, Solitary wave solutions of nonlinear wave equation,
American Journal of Physics 60(7) (1992), 650-654.
DOI: https://doi.org/10.1119/1.17120
[8] E. Fan and Y. C. Hona, Generalized tanh method extended to special
types of nonlinear equations, Zeitshrift fur Naturforschung A 57(8)
(2002), 692-700.
DOI: https://doi.org/10.1515/zna-2002-0809
[9] A. M. Wazwaz, The extended tanh method for new solitons solutions
for many forms of the fifth-order KdV equations, Applied Mathematics
and Computation 84(2) (2007), 1002-1014.
DOI: https://doi.org/10.1016/j.amc.2006.07.002
[10] C. A. Gomez and A. H. Salas, The Cole-Hopf transformation and
improved tanh-coth method applied to new integrable system (KdV6),
Applied Mathematics and Computation 204(2) (2008), 957-962.
DOI: https://doi.org/10.1016/j.amc.2008.08.006
[11] G. Garzon and S. Gomez, The generalized tanh-coth method applied
to biological model referent to nano-solitons of ionic wave, Applied
Mathematical Sciences 9(138) (2015), 6877-6882.
[12] M. Torvattanabun and S. Koonprasert, Variational iteration method
combined with the improved generalized tanh-coth method for the
generalized (1 + 1)-dimensional and (2+1) dimensional equations, Far
East Journal of Mathematical Sciences 100(8) (2016), 1339-1355.
DOI: http://dx.doi.org/10.17654/MS100081339
[13] M. Torvattanabun, J. Simmapim, D. Saennuad and T. Somaumchan, The
improved generalized tanh-coth method applied to sixth-order solitary
wave equation, Journal of Mathematics (2017); Article ID 8751097, 11
pages.
DOI: https://doi.org/10.1155/2017/8751097
[14] X.-J. Yang, Advanced Local Fractional Calculus and its
Applications, World Science Publisher, New York, 2012.
[15] X.-J. Yang, J. A. T. Machado and H. M. Srivastava, A new
numerical technique for solving the local fractional diffusion
equation: Two-dimensional extended differential transform approach,
Applied Mathematics and Computation 274 (2016), 143-151.
DOI: https://doi.org/10.1016/j.amc.2015.10.072
[16] S. Bibi, S. T. M. Din, R. Ullah, N. Ahmed and U. Khan, Exact
solutions for STO and (3 + 1)-dimensional KdV-ZK equations using
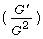 -expansion method, Results in Physics 7 (2017),
4434-4439.
-expansion method, Results in Physics 7 (2017),
4434-4439.
DOI: https://doi.org/10.1016/j.rinp.2017.11.009