Journal of Mathematical Sciences: Advances and Applications
METHOD AND NEW APPROACH OF GENERALIZED
METHOD FOR THE COUPLED RAMANI EQUATION[1] M. L. Wang, Solitary wave solutions for variant Boussinesq
equations, Physics Letters A 199(3-4) (1995), 169-172.
DOI: https://doi.org/10.1016/0375-9601(95)00092-H
[2] A. M. Wazwaz, A class of nonlinear fourth order variant of a
generalized Camassa-Holm equation with compact and noncompact
solutions, Applied Mathematics and Computation 165(2) (2005),
485-501.
DOI: https://doi.org/10.1016/j.amc.2004.04.029
[3] W. Malfliet and W. Hereman, The tanh method I: Exact solutions of
nonlinear evolution and wave equations, Physica Scripta 54(6) (1996),
563.
DOI: https://doi.org/10.1088/0031-8949/54/6/003
[4] A. M. Wazwaz, The tanh method: Exact solutions of the sine-Gordon
and the sinh-Gordon equations, Applied Mathematics and Computation
167(2) (2005), 1196-1210.
DOI: https://doi.org/10.1016/j.amc.2004.08.005
[5] S. Liu, Z. Fu, S. Liu and Q. Zhao, Jacobi elliptic function
expansion method and periodic wave solutions of nonlinear wave
equations, Physics Letters A 289(1-2) (2001), 69-74.
DOI: https://doi.org/10.1016/S0375-9601(01)00580-1
[6] M. L. Wang, X. Z. Li and J. L. Zhang, The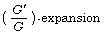 
method and travelling wave solutions in
mathematical physics, Physics Letters A 372(4) (2008), 417-423.
DOI: https://doi.org/10.1016/j.physleta.2007.07.051
[7] G. W. Bluman and J. D. Cole, Similarity Methods for Differential
Equations, Springer, Berlin, 1974.
[8] S. Y. Lou, X. R. Hu and Y. Chen, Nonlocal symmetries related to
Bäcklund transformation and their applications, Journal of Physics
A: Mathematical and Theoretical 45(15) (2012); Article 155209.
DOI: https://doi.org/10.1088/1751-8113/45/15/155209
[9] X. P. Xin, Y. T. Liu and X. Q. Liu, Nonlocal symmetries, exact
solutions and conservation laws of the coupled Hirota equations,
Applied Mathematics Letters 55 (2016), 63-71.
DOI: https://doi.org/10.1016/j.aml.2015.11.009
[10] V. B. Matveev and M. A. Salle, Darboux Transformations and
Solitons, Springer-Verlag, Berlin, 1991.
[11] H. Naher and F. A. Abdullah, New approach of 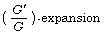method and new approach of generalized
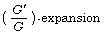method for nonlinear evolution equation, AIP
Advances 3(3) (2013); Article 032116.
DOI: https://doi.org/10.1063/1.4794947
[12] M. N. Alam and M. A. Akbar, The new approach of the generalized
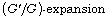method for nonlinear evolution equations, Ain
Shams Engineering Journal 5(2) (2014), 595-603.
DOI: https://doi.org/10.1016/j.asej.2013.12.008
[13] H. Naher, New approach of 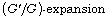method and new approach of generalized
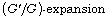method for ZKBBM equation, Journal of the
Egyptian Mathematical Society 23(1) (2015), 42-48.
DOI: https://doi.org/10.1016/j.joems.2014.03.005
[14] M. N. Alam, M. A. Akbar and K. Khan, Some new exact traveling
wave solutions to the (2 + 1)-dimensional breaking soliton equations,
World Applied Sciences Journal 25(3) (2013), 500-523.
[15] M. N. Alam and M. A. Akbar, Exact traveling wave solutions of the
KP-BBM equation by using the new generalized 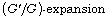method, SpringerPlus 2(1) (2013); Article
617.
DOI: https://doi.org/10.1186/2193-1801-2-617
[16] M. G. Hafez, M. N. Alam and M. A. Akbar, Exact traveling wave
solutions to the Klein-Gordon equation using the novel 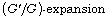method, Results in Physics 4 (2014),
177-184.
DOI: https://doi.org/10.1016/j.rinp.2014.09.001
[17] X. B. Hu, D. L. Wang and H. W. Tam, Lax pairs and Bäcklund
transformations for a coupled Ramani equation and its related system,
Applied Mathematics Letters 13(6) (2000), 45-48.
DOI: https://doi.org/10.1016/S0893-9659(00)00052-5
[18] J. X. Zhao and H. W. Tam, Solition solutions of a coupled Ramani
equation, Applied Mathematics Letters 19(4) (2006), 307-313.
DOI: https://doi.org/10.1016/j.aml.2005.01.006
[19] Y. He and H. W. Tam, Bilinear Bäcklund transformation and Lax
pair for a coupled Ramani equation, Journal of Mathematical Analysis
and Applications 357(1) (2009), 132-136.
DOI: https://doi.org/10.1016/j.jmaa.2009.04.006
[20] A. M. Wazwaz and H. Triki, Multiple soliton solutions for the
six-order Ramani equation and a coupled Ramani equation, Applied
Mathematics and Computation 216(1) (2010), 332-336.
DOI: https://doi.org/10.1016/j.amc.2010.01.067
[21] M. Chen, The symmetry reduction and exact solutions for the
coupled Ramani equations, Journal of Liaocheng University 24(3)
(2011), 1-4.
DOI: https://doi.org/10.3969/j.issn.1672-6634.2011.03.001
