Journal of Mathematical Sciences: Advances and Applications[1] L. M. Abia, J. C. López-Marcos and J. Martinez, On the blow-up
time convergence of semidiscretizations of reaction-diffusion
equations, Applied Numerical Mathematics 26(4) (1998), 399-414.
DOI: https://doi.org/10.1016/S0168-9274(97)00105-0
[2] T. K. Boni, Extinction for discretizations of some semilinear
parabolic equations, Comptes Rendus de l'Académie des Sciences,
Series I: Mathematics 333(8) (2001), 795-800.
DOI: https://doi.org/10.1016/S0764-4442(01)02078-X
[3] T. K. Boni, On blow-up and asymptotic behavior of solutions to a
nonlinear parabolic equation of second order with nonlinear boundary
conditions, Commentationes Mathematicae Universitatis Carolinae 40(3)
(1999), 457-475.
[4] T. K. Boni and Halima Nachid, Blow-up for semidiscretizations of
some semilinear parabolic equations with nonlinear boundary
conditions, Rev. Ivoir. Sci. Tech. 11 (2008), 61-70.
[5] T. K. Boni, Halima Nachid and Nabongo Diabate, Blow-up for
discretization of a localized semilinear heat equation, Analele
Stiintifice Ale Universitatii 2 (2010).
[6] H. Brezis, T. Cazenave, Y. Martel and A. Ramiandrisoa, Blow up for
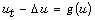revisited, Advances in Differential Equations
1(1) (1996), 73-90.
[7] Halima Nachid, Quenching for semi discretizations of a semilinear
heat equation with potentiel and general non linearities, Revue
d’Analyse Numerique et de Theorie de L’approximation 2
(2011), 164-181.
[8] Halima Nachid, Full discretizations of solution for a semilinear
heat equation with Neumann boundary condition, Research and
Communications in Mathematics and Mathematical Sciences 1(1) (2012),
53-85.
[9] Halima Nachid, L. B. Sobo Blin and Yoro Gozo, The blow-up time for
reaction-diffusion equations with dirichlet boundary conditions,
Journal of Multidisciplinary Engineering Science Studies 2(5) (2016),
483-493.
[10] A. Friedman and A. A. Lacey, The blow-up time for solutions of
nonlinear heat equations with small diffusion, SIAM Journal on
Mathematical Analysis 18(3) (1987), 711-721.
DOI: https://doi.org/10.1137/0518054
[11] A. Friedman and B. McCleod, Blow-up of positive solutions of
semilinear heat equations, Indiana University Mathematics Journal
34(2) (1985), 425-447.
DOI: https://doi.org/10.1512/iumj.1985.34.34025
[12] Y. Fujishima and K. Ishige, Blow-up set for a semilinear heat
equation with small diffusion, Journal of Differential Equations
249(5) (2010), 1056-1077.
DOI: https://doi.org/10.1016/j.jde.2010.03.028
[13] K. Ishige and H. Yagisita, Blow-up problems for a semilinear heat
equation with large diffusion, Journal of Differential Equations
212(1) (2005), 114-128.
DOI: https://doi.org/10.1016/j.jde.2004.10.021
[14] N. Mizoguchi and E. Yanagida, Life span of solutions for a
semilinear parabolic problem with small diffusion, Journal of
Mathematical Analysis and Applications 261(1) (2001), 350-368.
DOI: https://doi.org/10.1006/jmaa.2001.7530
[15] D. Nabongo and T. K. Boni, Numerical quenching for semilinear
parabolic equation, Mathematical Modelling and Analysis 13(4) (2008),
521-538.
DOI: https://doi.org/10.3846/1392-6292.2008.13.521-538
[16] D. Nabongo and T. K. Boni, Quenching time of solutions for some
nonlinear parabolic equations, Analele Stiintifice Ale Universitatii
“Ovidius†Constanta 16(1) (2008), 91-106.
[17] T. Nakagawa, Blowing up on the finite difference solution to
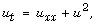Applied Mathematics and Optimization 2(4)
(1975), 337-350.
DOI: https://doi.org/10.1007/BF01448176
[18] M. H. Protter and H. F. Weinberger, Maximum Principles in
Differential Equations, Prentice Hall, Englewood Cliffs, NJ, 1967.
[19] R. Suzuki, On blow-up sets and asymptotic behavior of interface
of one dimensional quasilinear degenerate parabolic equations,
Publications of the Research Institute for Mathematical Sciences 27
(1991), 375-398.
[20] H. Yagisita, Blow-up profile of a solution for a nonlinear heat
equation with small diffusion, Journal of the Mathematical Society of
Japan 56(4) (2004), 993-1005.
DOI: https://doi.org/10.2969/jmsj/1190905445
[21] F. B. Weissler, An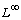 
blow-up estimate for a nonlinear heat equation,
Communications on Pure and Applied Mathematics 38(3) (1985),
291-295.
DOI: https://doi.org/10.1002/cpa.3160380303
[22] L. Wang and Q. Chen, The asymptotic behavior of blow-up solution
of localized nonlinear equations, Journal of Mathematical Analysis and
Applications 200(2) (1996), 315-321.
DOI: https://doi.org/10.1006/jmaa.1996.0207
