References

Journal of Mathematical Sciences: Advances and Applications

ON AN INEQUALITY RELATED TO THE RADIAL GROWTH OF QUASINEARLY SUBHARMONIC FUNCTIONS IN LOCALLY UNIFORMLY HOMOGENEOUS SPACES

[1] Ronald R. Coifman and Guido Weiss, Analyse Harmonique Non-commutative Sur Certains Espaces Homogènes, Lecture Notes in Mathematics, Vol. 242, Springer, Berlin, Heidelberg, New York, 1971.

[2] Ronald R. Coifman and Guido Weiss, Extensions of Hardy spaces and their use in analysis, Bull. Amer. Math. Soc. 83(4) (1977), 569-645.

[3] G. David and S. Semmes, Analysis of and on Uniformly Rectifiable Sets, Mathematical Surveys and Monographs, Vol. 38, American Mathematical Society, Providence, Rhode Island, 1991.

[4] O. Dovgoshey and J. Riihentaus, Bi-Lipschitz and quasi-nearly subharmonic functions, International Journal of Mathematics and Mathematical Sciences/New Trends in Geometric Function Theory 2010 (2010), Article ID 382179, 8 pages, (doi:10.1155/2010/382179).

[5] O. Dovgoshey and J. Riihentaus, A remark concerning generalized mean value inequalities for subharmonic functions, submitted.

[6] C. Fefferman and E. M. Stein, 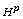spaces of several variables, Acta Math. 129 (1972), 137-192.

[7] F. W. Gehring, On the radial order of subharmonic functions, J. Math. Soc. Japan 9 (1957), 77-79.

[8] Zbigniew Grande, Quasicontinuity and measurability of functions of two variables, Real Analysis Exchange 28 (2002), 7-14.

[9] D. J. Hallenbeck, Radial growth of subharmonic functions, Pitman Research Notes 262 (1992), 113-121.

[10] M. Hervé, Analytic and Plurisubharmonic Functions in Finite and Infinite Dimensional Spaces, Lecture Notes in Mathematics, Vol. 198, Springer-Verlag, Berlin, 1971.

[11] B. E. Johnson, Separate continuity and measurability, Proc. Amer. Math. Soc. 20 (1969), 420-422.

[12] V. Kojić, Quasi-nearly subharmonic functions and conformal mappings, Filomat. 21(2) (2007), 243-249.

[13] Ü. Kuran, Subharmonic behavior of 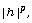( 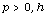harmonic), J. London Math. Soc. 8(2) (1974), 529-538.

[14] Jaroslav Lukeš and Jan Malý, Measure and Integral, Matfyzpress, Publishing House of the Faculty of Mathematics and Physics, Charles University, Prague, 1995.

[15] Pertti Mattila, Geometry of Sets and Measures in Euclidean Spaces, Cambridge Studies in Advanced Mathematics, Vol. 44, Cambridge University Press, Cambridge, 1995.

[16] Y. Mizuta, Boundary limits of functions in weighted Lebesgue or Sobolev classes, Revue Roum. Math. Pures Appl. 46 (2001), 67-75.

[17] M. Pavlović, Mean values of harmonic congugates in the unit disc, Complex Variables 10 (1988), 53-65.

[18] M. Pavlović, On subharmonic behavior and oscillation of functions on balls in 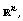Publ. Inst. Math. (Beograd) 55(69) (1994), 18-22.

[19] M. Pavlović, On subharmonic behavior of smooth functions, Matematichki Vesnik 48 (1996), 15-21.

[20] M. Pavlović and J. Riihentaus, Classes of quasi-nearly subharmonic functions, Potential Anal. 29 (2008), 89-104.

[21] M. Pavlović, An inequality related to Gehring-Hallenbeck theorem on radial limits of functions in harmonic Bergman spaces, Glasgow Math. J. 50(3) (2008), 433-435.

[22] M. Pavlović and J. Riihentaus, Quasi-nearly subharmonic functions in locally uniformly homogeneous spaces, Positivity, to appear, (doi:10.1007/s11117-009-0037- 0).

[23] J. Riihentaus, On a theorem of Avanissian-Arsove, Expo. Math. 7 (1989), 69-72.

[24] J. Riihentaus, Subharmonic functions: Non-tangential and tangential boundary behavior, Function Spaces, Differential Operators and Nonlinear Analysis (FSDONA’99), Proceedings of the Syöte Conference 1999, V. Mustonen, J. Rákosnik (eds.), Math. Inst., Czech Acad. Science, Praha, (2000), 229-238.

[25] J. Riihentaus, A generalized mean value inequality for subharmonic functions, Expo. Math. 19 (2001), 187-190.

[26] J. Riihentaus, Subharmonic functions, mean value inequality, boundary behavior, nonintegrability and exceptional sets, International Workshop on Potential Theory and Free Boundary Flows, Kiev, Ukraine, August 19-27, 2003, Transactions of the Institute of Mathematics of the National Academy of Sciences of Ukraine 1(1) (2004), 169-191.

[27] J. Riihentaus, Weighted boundary behavior and nonintegrability of subharmonic functions, International Conference on Education and Information Systems: Technologies and Applications (EISTA’04), Orlando, Florida, USA, July 21-25, 2004, Proceedings, M. Chang, Y.-T. Hsia, F. Malpica, M. Suarez, A. Tremante, F. Welsch (eds.), Vol. II, 2004, pp. 196-202.

[28] J. Riihentaus, A weighted boundary limit result for subharmonic functions, Adv. Algebra and Analysis 1 (2006), 27-38.

[29] J. Riihentaus, Separately quasi-nearly subharmonic functions, Complex Analysis and Potential Theory, Proceedings of the Conference Satellite to ICM 2006, Tahir Aliyev AzeroÄŸlu, Promarz M. Tamrazov (eds.), Gebze Institute of Technology, Gebze, Turkey, September 8-14, 2006, World Scientific, Singapore, (2007), 156-165.

[30] J. Riihentaus, Subharmonic functions, generalizations and separately subharmonic functions, 14th Conference on Analytic Functions, July 22-28, 2007, Chełm, Poland, Scientific Bulletin of Chełm, Section of Mathematics and Computer Science 2 (2007), 49-76, (arXiv:math/0610259v5 [math.AP] 8 Oct 2008).

[31] J. Riihentaus, Quasi-nearly subharmonicity and separately quasi-nearly subharmonic functions, J. Inequal. Appl. 2008 (2008), Article ID 149712, 15 pages, (doi: 10.1155/2008/149712) (arXiv:0802.3505v2 [math.AP] 16 Oct 2008).

[32] J. Riihentaus, On an inequality related to the radial growth of subharmonic functions, Cubo, A Mathematical Journal 11(4) (2009), 127-136.

[33] J. Riihentaus, Subharmonic functions, generalizations, weighted boundary behavior, and separately subharmonic functions: A survey, Fifth World Congress of Nonlinear Analysts (WCNA 2008), Orlando, Florida, USA, July 2-9, 2008, Nonlinear Analysis, Series A: Theory, Methods & Applications 71(12) (2009), 2613-2627.

[34] Walter Rudin, Lebesgue’s First Theorem, Mathematical Analysis and Applications, Part B, pp. 741-747, Advances in Mathematics Supplementary Studies, Vol. 7B, Academic Press, New York, London, 1981.

[35] W. Sierpiński, Sur un problème concernant les ensembles mesurables superficiellement, Fund. Math. 1 (1920), 112-115.

[36] M. Stoll, Invariant Potential Theory in the Unit Ball of 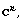London Mathematical Society Lecture Notes Series, Cambridge, 1994.

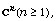[37] M. Stoll, Boundary limits and non-integrability of -subharmonic functions in the unit ball of Trans. Amer. Math. Soc. 349 (1997), 3773-3785.

[38] M. Stoll, Weighted tangential boundary limits of subharmonic functions on domains in 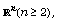Math. Scand. 83 (1998), 300-308.

[39] A. Torchinsky, Real-Variable Methods in Harmonic Analysis, Academic Press, London, 1986.

[40] M. Vuorinen, On the Harnack constant and the boundary behavior of Harnack functions, Ann. Acad. Sci. Fenn., Ser. A I, Math. 7 (1982), 259-277.