[1] E. Camouzis and G. Ladas, Dynamics of Third-Order Rational
Difference Equations with Open Problems and Conjectures, Chapman and
Hall/CRC, 2007.
[2] E. Camouzis and G. Ladas, When does local asymptotic stability
imply global attractivity in rational equations?, Journal of
Difference Equations and Applications 12(8) (2006), 863-885.
DOI: https://doi.org/10.1080/10236190600772663
[3] M. Dipippo, Global Dynamics of Some Quadratic Difference
Equations, University of Rhode Island, 2016.
[4] H. El-Metwally, E. A. Grove and G. Ladas, A global convergence
result with applications to periodic solutions, Journal of
Mathematical Analysis and Applications 245(1) (2000), 161-170.
DOI: https://doi.org/10.1006/jmaa.2000.6747
[5] E. M. Elabbasy, H. El-Metwally and E. M. Elsayed, Global
attractivity and periodic character of a fractional difference
equation of order three, Yokohama Mathematical Journal 53 (2007),
89-100.
[6] H. El-Metwally, Qualitative properties of some higher order
difference equations, Computers & Mathematics with Applications 58(4)
(2009), 686-692.
DOI: https://doi.org/10.1016/j.camwa.2009.03.092
[7] H. El-Metwally and E. M. Elsayed, Qualitative behavior of some
rational difference equations, Journal of Computational Analysis and
Applications 20(2) (2016), 226-236.
[8] E. M. Elsayed and H. El-Metwally, Global behavior and periodicity
of some difference equations, Journal of Computational Analysis and
Applications 19(2) (2015), 298-309.
[9] H. El-Metwally, I. Yalcinkaya and C. Cinar, Global stability of an
economic model, Utilitas Mathematica 95 (2014), 235-244.
[10] M. Garić-Demirović, M. R. S. Kulenović and M.
Nurkanović, Global dynamics of certain homogeneous second-order
quadratic fractional difference equation, The Scientific World Journal
(2013), Article ID 210846, pages 1-10.
DOI: http://dx.doi.org/10.1155/2013/210846
[11] M. Garić-Demirović, M. R. S. Kulenović and M.
Nurkanović, Basins of attraction of equilibrium points of second
order difference equations, Applied Mathematics Letters 25(12) (2012),
2110-2115.
DOI: https://doi.org/10.1016/j.aml.2012.05.009
[12] C. Gibbons, M. R. S. Kulenović and G. Ladas, On the recursive
sequence 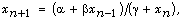 Mathematical Sciences Research Hotline 4(2)
(2000), 1-11.
Mathematical Sciences Research Hotline 4(2)
(2000), 1-11.
[13] S. J. Hrustić, M. R. S. Kulenović and M. Nurkanović,
Global dynamics and bifurcations of certain second order rational
difference equation with quadratic terms, Qualitative Theory of
Dynamical Systems 15(1) (2016), 283-307.
DOI: https://doi.org/10.1007/s12346-015-0148-x
[14] S. Jašarević and M. R. S. Kulenović, Basins of
attraction of equilibrium and boundary points of second-order
difference equations, Journal of Difference Equations and Applications
20(5-6) (2014), 947-959.
DOI: https://doi.org/10.1080/10236198.2013.855733
[15] S. Kalabušic, M. R. S. Kulenović and E. Pilav, Global
dynamics of anti-competitive systems in the plane, Dynamics of
Continuous, Discrete and Impulsive Systems Series A: Mathematical
Analysis 20(4) (2013), 477-505.
[16] M. R. S. Kulenović and G. Ladas, Dynamics of second order
rational difference equations: With open problems and conjectures,
Chapman and Hall/CRC, 2001.
[17] M. R. S. Kulenović, S. Moranjkic and Z. Nurkanovic,
Naimark-Sacker bifurcation of second order rational difference
equation with quadratic terms, Journal of Nonlinear Sciences and
Applications 10(7) (2017), 3477-3489.
DOI: http://dx.doi.org/10.22436/jnsa.010.07.11
[18] M. R. S. Kulenović, and O. Merino, Global bifurcation for
discrete competitive systems in the plane, Discrete & Continuous
Dynamical Systems-B 12(1) (2009), 133-149.
DOI: http://dx.doi.org/10.3934/dcdsb.2009.12.133
[19] M. R. S. Kulenović, and O. Merino, Invariant manifolds for
competitive discrete systems in the plane, International Journal of
Bifurcation and Chaos 20(8) (2010), 2471-2486.
DOI: https://doi.org/10.1142/S0218127410027118
[20] M. R. S. Kulenović, S. Moranjkić and Z. Nurkanović,
Global dynamics and bifurcation of a perturbed Sigmoid Beverton-Holt
difference equation, Mathematical Methods in the Applied Sciences
39(10) (2016), 2696-2715.
DOI: https://doi.org/10.1002/mma.3722
[21] M. R. S. Kulenović and O. Merino, Discrete Dynamical Systems
and Difference Equations with Mathematica, CRC Press, 2002.
[22] G. L. Karakostas, A discrete semi-flow in the space of sequences
and study of convergence of sequences defined by difference equations,
M. E. Greek Math. Soc. 30 (1989), 66-74.
[23] M. Pituk, More on Poincaré’s and Perron’s
Theorems for Difference Equations, Journal of Difference Equations and
Applications 8(3) (2002), 201-216.
DOI: https://doi.org/10.1080/10236190211954