Journal of Mathematical Sciences: Advances and Applications
EQUATION[1] P. Rosenau and J. M. Hyman, Solutions with finite wavelengths,
Physical Review Letters 70(5) (1993), 564-567.
DOI: https://doi.org/10.1103/PhysRevLett.70.564
[2] A. M. Wazwaz, General compactons solutions and solitary patterns
solutions for modified nonlinear dispersive equations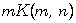 
in higher dimensional spaces, Mathematics and
Computers in Simulation 59(5) (2002), 519-531.
DOI: https://doi.org/10.1016/S0378-4754(01)00439-6
[3] Y. Chen, B. Li and H. Q. Zhang, New exact solutions for modified
nonlinear dispersive equations 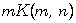in higher dimensions spaces, Mathematics and
Computers in Simulation 64(5) (2004), 549-559.
DOI: https://doi.org/10.1016/j.matcom.2003.10.005
[4] F. D. Xie, X. Sh. Gao and F. Liu, Conservation laws of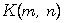 
and 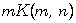equations, Communications in Theoretical
Physics 42(5) (2004), 661-663.
DOI: https://doi.org/10.1088/0253-6102/42/5/661
[5] S. Y. Lai, J. B. He and Y. Qing, A new study for the modified
nonlinear dispersive 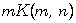equations in higher dimensional spaces,
International Journal of Pure and Applied Mathematics 51(1) (2009),
1-9.
[6] Y. X. Yu, New compacton solutions and solitary pattern solutions
for modified nonlinearly dispersive mK(m, n,
a, b) equation, Communications in Theoretical Physics
52(4) (2009), 637-640.
DOI: https://doi.org/10.1088/0253-6102/52/4/17
[7] W. Malfliet, Solitary wave solutions of nonlinear wave equations,
American Journal of Physics 60(7) (1992), 650-654.
DOI: https://doi.org/10.1119/1.17120
[8] W. Malfliet and W. Hereman, The tanh method I: Exact solutions of
nonlinear evolution and wave equations, Physica Scripta 54(6) (1996),
563-568.
DOI: https://doi.org/10.1088/0031-8949/54/6/003
[9] W. Malfliet and W. Hereman, The tanh method II: Perturbation
technique for conservative systems, Physica Scripta 54(6) (1996),
569-575.
DOI: https://doi.org/10.1088/0031-8949/54/6/004
[10] W. Hereman and W. Malfliet, The Tanh method: A tool to solve
nonlinear partial differential equations with symbolic software,
Proceedings 9th World Multi-Conference on Systemics, Cybernetics and
Informatics, Orlando, FL (2005), 165-168.
[11] E. G. Fan, Extended tanh-function method and its applications to
nonlinear equations, Physics Letters A 277(4-5) (2000), 212-218.
DOI: https://doi.org/10.1016/S0375-9601(00)00725-8
[12] Z. S. Lu and H. Q. Zhang, On a new modified extended
tanh-function method, Communications in Theoretical Physics 39(4)
(2003), 405-408.
DOI: https://doi.org/10.1088/0253-6102/39/4/405
[13] E. M. E. Zayed and K. A. E. Alurrfi, The modified extended
tanh-function method and its applications to the generalized KdV-mKdV
equation with any-order nonlinear terms, International Journal of
Environmental Engineering Science and Technology Research 1(8) (2013),
165-170.
[14] E. H. M. Zahran and M. M. A. Khater, Modified extended
tanh-function method and its applications to the Bogoyavlenskii
equation, Applied Mathematical Modelling 40(3) (2016), 1769-1775.
DOI: https://doi.org/10.1016/j.apm.2015.08.018
