Journal of Mathematical Sciences: Advances and Applications[1] F. Chyzak, A. Quadrat and D. Robertz, Effective algorithms for
parametrizing linear control systems over Ore algebras, AAECC 16
(2005), 319-376.
[2] T. Cluzeau and A. Quadrat, Factoring and decomposing a class of
linear functional systems, Lin. Alg. and its Appl. 428 (2008),
324-381.
[3] A. Fabiańska and A. Quadrat, Applications of the Quillen-Suslin
theorem to multirankal systems theory, INRIA, Rapport de Recherche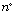
6126 (2007).
[4] J. Gago-Vargas, On Suslin’s Stability Theorem for 
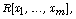Ring Theory and Algebraic Geometry, Lecture
Notes in Pure and Applied Mathematics, Vol. 221, Marcel Dekker, New
York, (2001), 203-210.
[5] G. Greuel and G. Pfister, A Singular Introduction to Commutative
Algebra, 2nd edition, Springer, 2007.
[6] T. Y. Lam, Serre’s Problem on Projective Modules, Springer
Monographs in Mathematics, Springer, 2006.
[7] S. Lang, Algebra, Springer, 2004.
[8] R. C. Laubenbacher and C. Woodburn, An algorithm for the
Quillen-Suslin theorem for monoid rings, J. Pure Appl. Algebra 117-118
(1997), 395-429.
[9] R. C. Laubenbacher and K. Schlauch, An algorithm for the
Quillen-Suslin theorem for quotients of polynomial rings by monomial
ideals, J. Symb. Comp. 30 (2000), 555-571.
[10] R. C. Laubenbacher and C. Woodburn, A new algorithm for the
Quillen-Suslin theorem, Contributions to Algebra and Geometry 41
(2000), 23-31.
[11] O. Lezama, Gröbner bases for modules over Noetherian polynomial
commutative rings, Georgian Mathematical Journal 15 (2008),
121-137.
[12] O. Lezama, Some applications of Gröbner bases in homological
algebra, São Paulo Journal of Mathematical Sciences 3(1)
(2009), 25-59.
[13] O. Lezama et al., Quillen-Suslin rings, Extracta Mathematicae
24(1) (2009).
[14] A. Logar and B. Sturmfels, Algorithms for the Quillen-Suslin
theorem, J. Algebra 145(1) (1992).
[15] H. Lombardi, Le contenu constructif d’un principe local-global
avec une application á la structure d’un module projectif de type
fini, Laboratoire de Mathématiques de Besançon, Université de
Franche-Comté, 1997.
[16] H. Lombardi and Quitté, Algèbre Commutative, Méthodes
Constructives, Modules Projectifs de Type Fini, 2009:
hlombardi.free.fr/
[17] B. MacDonald, Linear Algebra over Commutative Rings, Marcel
Dekker, 1984.
[18] H. Park and C. Woodburn, An algorithmic proof of Suslin’s
stability theorem for polynomial rings, J. Algebra 178 (1995),
277-298.
[19] A. Quadrat and D. Robertz, Computation of bases of free modules
over the Weyl algebras, Journal of Symbolic Computation (2007),
doi:10.1016/j.jsc.2007.06.005.
[20] D. Quillen, Projective modules over polynomial rings, Invent.
Math. 36 (1976), 167-171.
[21] J. J. Rotman, An Introduction to Homological Algebra, Academic
Press, 1979.
[22] A. A. Suslin, Projective modules over polynomial rings are free,
Soviet Math. Dokl. 17 (1976), 1160-1164.
