Journal of Mathematical Sciences: Advances and Applications[1] R. P. Agarwal, Difference Equations and Inequalities, Second Ed.,
Dekker, New York, 1992, 2000.
[2] L. Berg, On the asymptotics of nonlinear difference equations, Z.
Anal. Anwendungen 21 (2002), 1061-1074.
[3] L. Berg, Oscillating solutions of rational difference equations,
Rostock. Math. Kolloq. 58 (2004), 31-35.
[4] V. L. Kocic and G. Ladas, Global Behavior of Nonlinear Difference
Equations of Higher Order with Applications, Kluwer Academic,
Dordrecht, 1993.
[5] M. R. S. Kulenović, G. Ladas, L. F. Martins and I. W. Rodrignes,
The dynamics of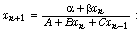 
Facts and conjectures, Comput. Math. Appl.
45 (2003), 1087-1099.
[6] G. Ladas, Progress report on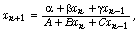 
J. Differ. Equations Appl. 1 (1995),
211-215.
[7] X. Li, Qualitative properties for a fourth-order rational
difference equation, J. Math. Anal. Appl. 311 (2005), 103-111.
[8] S. Stević, Asymptotic behaviour of a sequence defined by a
recurrence formula, Austral. Math. Soc. Gaz. 28 (2001), 243-245.
[9] S. Stević, A note on the difference equation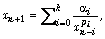 
J. Differ. Equations Appl. 8 (2002),
641-647.
[10] S. Stević and K. Berenhaut, A note on positive nonoscillatory
solutions of the difference equation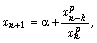 
J. Differ. Equations Appl. 12 (2006),
495-499.
