Journal of Mathematical Sciences: Advances and Applications[1] A. Alonso and A. Valli, An optimal domain decomposition
preconditioner for low-frequency time-harmonic Maxwell equations,
Math. Comput. 68(226) (1999), 607-631.
DOI: https://doi.org/10.1090/S0025-5718-99-01013-3
[2] A. Bossavit, Computational Electromagnetism, Academic Press, San
Diego, 1998.
[3] A. Bossavit, Mixed Finite Elements and the Complex of Whitney
Forms, Academic Press, London, 1988.
[4] F. Brezzi, J. Douglas, R. Duran and M. Fortin, Mixed finite
elements for second order elliptic problems in three variables, Numer.
Math. 51(2) (1987), 237-250.
DOI: https://doi.org/10.1007/BF01396752
[5] J. H. Kim and Do Y. Kwak, New curl conforming finite elements on
parallelepiped, Numer. Math. 131(3) (2015), 473-488.
DOI: https://doi.org/10.1007/s00211-015-0696-7
[6] J. H. Kim, New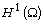 
conforming finite elements on hexahedra, Int.
J. Pure Appl. Math. 109(3) (2016), 609-618.
DOI: https://doi.org/10.12732/ijpam.v109i3.10
[7] J. C. Nedelec, Mixed finite elements in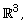 
Numer. Math. 35(3) (1980), 315-341.
DOI: https://doi.org/10.1007/BF01396415
[8] Philippe G. Ciarlet, The Finite Element Method for Elliptic
Problems, North-Holland Publishing Company, New York, 1978.
[9] Peter Monk, Finite Element Methods for Maxwell’s Equations,
Clarendon Press, Oxford, 2003.
[10] Peter Monk, Analysis of a finite element method for
Maxwell’s equations, SIAM J. Numer. Anal. 29(3) (1992),
714-729.
DOI: https://doi.org/10.1137/0729045
