Journal of Mathematical Sciences: Advances and Applications[1] S. Aytar and S. Pehlivan, Statistically monotonic and
statistically bounded sequences of fuzzy numbers, Inf. Sci. 176
(2006), 734-744.
[2] P. Diamond and P. Kloeden, Metric Spaces of Fuzzy Sets: Theory and
Applications, World Scientific, Singapore, 1994.
[3] D. Dubois and H. Prade, Fuzzy Sets and Systems: Theory and
Applications, Academic Pres, New York, 1980.
[4] R. Goetschel and W. Voxman, Elementary fuzzy calculus, Fuzzy Sets
and Systems 18 (1986), 31-43.
[5] J. S. Kwon, On statistical and p-Cesaro convergence of
fuzzy numbers, Korean J. Comput. Appl. Math. 7(1) (2000), 195-203.
[6] M. Matloka, Sequences of fuzzy numbers, Busefal 28 (1986),
28-37.
[7] S. Nanda, On sequences of fuzzy numbers, Fuzzy Sets and Systems 33
(1989), 123-126.
[8] F. Nuray, Lacunary statistical convergence of sequences of fuzzy
numbers, Fuzzy Sets and Systems 99 (1998), 353-356.
[9] E. Savas, On strongly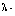 
summable sequences of fuzzy numbers, lnform.
Sci. 125 (2000), 181-186.
[10] N. Tuncer and F. B. Benli, 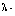Statistical limit points of the sequences of
fuzzy numbers, Inform. Sci. 177 (2007), 3297-3304.
[11] C. Wu and G. Wang, Convergence of sequences of fuzzy numbers and
fixed point theorems for increasing fuzzy mappings and application,
Fuzzy Sets and Systems 130 (2002), 383-390.
[12] L. A. Zadeh, Fuzzy sets, Information and Control 8 (1965),
338-353.
