Journal of Mathematical Sciences: Advances and Applications[1] N. Bozhinov, Convolutional Representations of Commutants and
Multipliers (Sofia), 1988.
[2] I. Dimovski, Convolutional Calculus, Kluwer Academic Publishers,
Dordrecht, 1990.
[3] M. K. Fage and N. I. Nagnibida, Problem of Equivalence of Linear
Ordinary Differential Operators, Nauka, Novosibisk, 1987.
[4] M. Gürdal, Description of extended eigenvalues and extended
eigenvectors of integration operator on the Wiener algebra, Expo.
Math. 27(2) (2009), 153-160.
[5] M. T. Karaev and H. Tuna, Description of maximal ideal space of
some Banach algebra with multiplication as Duhamel product, Complex
Variables 49(6) (2004), 449-457.
[6] M. T. Karaev and S. Saltan, A Banach algebra structure for the
Wiener algebra W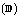 
of the disc, Complex Variables: Theory and
Applications 50 (2005), 299-305.
[7] M. A. Lavrent’ev and B. V. Shabat, Methods of the Theory of
Functions of Complex Variable, Nauka, 1973 (in Russian).
[8] K. G. Merryfield and S. Watson, A local algebra structure for
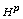of the polydisc, Colloq. Math. 62 (1991),
73-79.
[9] J. Mikusinski, Operational Calculus, Pergemon Press,
Oxford-Warszawa, 1956.
[10] N. I. Nagnibida, Description of commutants of integration
operator in analytic spaces, Sib. Mat. Zh. 5(22) (1981), 125-131.
[11] V. A. Tkachenko, Operators that commute with generalized
integration in spaces of analytic functionals, Math. Zametki 25(2)
(1979), 271-282.
[12] N. M. Wigley, The Duhamel product of analytic functions, Duke
Math. J. 41 (1974), 211-217.
[13] N. M. Wigley, A Banach algebra structure for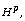 
Canad. Math. Bull. 18 (1975), 597-603.
