Journal of Mathematical Sciences: Advances and Applications
HOMOGENEOUS STRONGLY LOCAL FORMS[1] M. Biroli and N. Tchou, Asymptotic behavior of relaxed Dirichlet
problems involving a Dirichlet-Poincaré form, J. Anal. Appl. 16
(1997), 281-309.
[2] M. Biroli, C. Picard and N. Tchou, Homogenization of the
p-Laplacian associated with the Heisenberg group, Mem. di Mat.,
Rend. Acc. Naz. Sc. Detta dei XL 22 (1998), 23-42.
[3] M. Biroli and N. Tchou, Relaxed Dirichlet problem for the
subelliptic p-Laplacian, Ann. Mat. Pura Appl. (IV), CLXXIX
(2001), 39-64.
[4] M. Biroli, C. Picard and N. Tchou, Asymptotic behavior of some
nonlinear subelliptic Dirichlet problems, Mem. di Mat., Rend. Acc.
Naz. Sc. Detta dei XL 26 (2002), 235-252.
[5] M. Biroli and P. Vernole, Strongly local nonlinear Dirichlet
functionals and forms, Adv. Math. Sci. Appl. 15 (2005), 655-682.
[6] M. Biroli and P. Vernole, A priori estimates for
p-Laplacian associated with nonlinear Dirichlet forms,
Nonlinear Analysis 64 (2006), 51-68.
[7] L. Boccardo and F. Murat, Almost everywhere convergence of the
gradients of solutions to elliptic and parabolic equations, Nonlinear
Analysis 19 (1992), 581-597.
[8] F. Dal Fabbro and S. Marchi,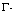 
convergence of strongly local Dirichlet
functionals, Riv. Mat. Univ. Parma, (in print).
[9] G. Dal Maso and F. Murat, Asymptotic behaviour and correctors for
Dirichlet problems in perforated domains with homogeneous monotone
operators, Ann. Sc. Norm. Sup. Pisa 24 (1979), 239-290.
[10] J. Maly and U. Mosco, Remarks on measure-valued Lagrangians on
homogeneous spaces, Ricerche Mat. 48 (Supp.) (1999), 217-231.
