Journal of Mathematical Sciences: Advances and Applications[1] Ch. G. Philos, On the existence of nonoscillatory solutions
tending to zero at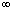 
for differential equations with positive
delays, Arch. Math. 36 (1981), 168-178.
[2] B. Karpuz, Ö. Öcalan and S. Öztürk, Comparison
theorems on the oscillation and asymptotic behaviour of high-order
neutral differential equations, Glasgow Math. J. 52 (2010),
107-114.
[3] R. P. Agarwal, S. R. Grace and D. O’Regan, Oscillation
Theory for Difference and Functional Differential Equations, Marcel
Dekker, Kluwer Academic, Dordrecht, 2000.
[4] R. P. Agarwal, S. R. Grace and D. O’Regan, Oscillation
Theory for Second Order Linear, Half-linear, Superlinear and Sublinear
Dynamic Equations, Kluwer Academic Publishers, Dordrecht, 2002.
[5] J. Manojlović, Oscillation criteria for second order
half-linear differential equations, Math. Comp. Model. 30 (1999),
109-119.
[6] S. H. Saker, Oscillation Theory of Delay Differential and
Difference Equations, Second and Third Orders, VDW Verlag Dr.
Müller, 2010.
[7] Ch. G. Philos, A new ctiterion for the oscillatory and asymptotic
behaviour of delay differential equations, Bull. Acad. Pol. Sci.
Sér. Sci. Math. 39 (1981), 61-64.
[8] B. BaculÃková and J. Džurina, Oscillation theorems for
higher order neutral differential equations, Appl. Math. Comp. 219
(2012), 3769-3778.
[9] I. T. Kiguradze and T. A. Chanturiya, Asymptotic Properties of
Solutions of Nonautonomous Ordinary Differential Equations, Kluwer
Academic Publishers, Dordrecht, 1993; Translated from the 1985 Russian
original.
[10] R. P. Agarwal, S. R. Grace and D. O’Regan, The oscillation
of certain high-order functional differential equations, Math. Comput.
Model. 37 (2003), 705-728.
