Journal of Mathematical Sciences: Advances and Applications[1] S. Barnett and R. G. Cameron, Introduction to Mathematical Control
Theory, Clarendon Press, Oxford, 1985.
[2] I. I. Blekhman, A. L. Fradkov, H. Nijimeijer and A. Y. Pogromsky,
On self-synchronization and controlled synchronization, Syst. Control
Lett. 31 (1997), 299-305.
[3] I. I. Blekhman, A. L. Fradkov, O. P. Tomchina and D. E. Bogdanov,
Self-synchronization and controlled synchronization: General
definition and example design, Math. Comput. Simul. 58 (2002),
367-384.
[4] G. Chen and X. Dong, From Chaos to Order: Methodologies,
Perspectives and Applications, World Scientific, Singapore, 1998.
[5] G. Chen and J. Lu, Dynamics of the Lorenz System Family: Analysis,
Control and Synchronization, Science Press, Beijing, China, 2003.
[6] D. V. Efimov and A. L. Fradkov, Adaptive nonlinear partial
observers with application to time-varying chaotic systems, IEEE Conf.
Control Applications, Istanbul, (2003), 23-25.
[7] A. L. Fradkov, Adaptive synchronization of hyper-minimum-phase
systems with nonlinearities, Proc. of 3rd IEEE Mediterranean Symp. on
New Directions in Control, Limassol 1 (1995), 272-277.
[8] A. L. Fradkov, V. O. Nikiforov and B. R. Andrievsky, Adaptive
observers for nonlinear nonpassifiable systems with application to
signal transmission, Proc. of 41th IEEE Conf. Decision and Control,
Las Vegas, December 10-13 (2002), 4706-4711.
[9] Y. H. Liu, S. Arimoto, V. Parra-Vega and K. Kitagaki,
Decentralized adaptive control of multiple manipulators in
cooperations, Int. J. Control 67 (1997), 649-673.
[10] H. Nijimeijer, A dynamical control view on synchronization,
Physica D 154 (2001), 219-228.
[11] L. Pecora and T. Carrol, Synchronization in chaotic systems,
Phys. Rev. Lett. 64 (1990), 821-824.
[12] V. N. Phat, Introduction to Mathematical Control Theory, Hanoi
National University Publisher, Hanoi, 2001.
[13] V. N. Phat, N. M. Linh and T. D. Phuong, Sufficient conditions
for strong stability of nonlinear time-varying control systems with
state delays, Acta Math. Vietnamica 30 (2005), 69-86.
[14] V. N. Phat and Q. P. Ha,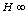 
control and exponential stability for a
class of nonlinear non-autonomous systems with time-varying delay, J.
Optim. Theory Appl. 142 (2009), 603-618 (SCI).
[15] A. Pikovsky, M. Rosenblum and J. Kurths, Synchronization, a
Universal Concept in Nonlinear Sciences, Cambridge University Press,
Cambridge, London, 2001.
[16] A. Y. Pogromsky, G. Santoboni and H. Nijimeijer, Partial
synchronization: From symmetry toward stability, Physica D 172 (2002),
65-87.
[17] G. Santoboni, A. Y. Pogromsky and H. Nijimeijer, Partial observer
and partial synchronization, Int. J. Bifurcation Chros 13 (2003), 453-
458.
