Journal of Mathematical Sciences: Advances and Applications
DIMENSIONAL NONLINEAR EVOLUTION EQUATIONS
USING THE EXTENDED TANH METHOD[1] M. J. Ablowitz and P. A. Clarkson, Solitons, Nonlinear Evolution
Equations and Inverse Scattering, Cambridge University Press, London,
1991.
[2] G. W. Bluman and S. Kumei, Symmetries and Differential Equations,
Springer-Verlag, Berlin, 1989.
[3] E. G. Fan, Uniformly constructing a series of explicit exact
solutions to nonlinear equations in mathematical physics, Chaos
Solitons and Fractals 16 (2003), 819-839.
[4] C. H. Gu, H. S. Hu and Z. X. Zhou, Darboux Transformations in
Soliton Theory and its Geometric Applications, Shanghai Sci. Tech.
Publ., Shanghai, 1999.
[5] R. Hirota and J. Satsuma, Soliton solutions of a coupled KdV
equation, Phys. Lett. A 85 (1981), 407-408.
[6] J. B. Li and Z. Liu, Travelling wave solutions for a class of
nonlinear dispersive equations, Chin. Ann. Math. 23B (2002),
397-418.
[7] W. Malfliet, Solitary wave solutions of nonlinear wave equations,
Amer. J. Phys. 60(7) (1992), 650-654.
[8] W. Malfliet and W. Hereman, The tanh method: II Perturbation
technique for conservative systems, Phys. Scr. 54 (1996), 569-575.
[9] V. B. Matveev and M. A. Salle, Darboux Transformation and
Solitons, Springer-Verlag, Berlin, 1991.
[10] P. J. Olver, Applications of Lie Groups to Differential
Equations, Springer-Verlag, New York, 1993.
[11] S. Tang and W. Huang, Bifurcations of travelling wave solutions
for the generalized double sinh-Gordon equation, Appl. Math. Comput.
189 (2007), 1774-1781.
[12] F. Tascana and A. Bekir, Analytic solutions of the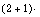 
dimensional nonlinear evolution equations
using the sine-cosine method, Appl. Math. Comput. (2009), in press.
[13] L. Tian and J. Yin, New compacton solutions and solitary wave
solutions of fully nonlinear generalized Camassa-Holm equations, Chaos
Solitons and Fractals 20 (2004), 289-299.
[14] M. L. Wang, Exact solutions for a compound KdV-Burgers equation,
Phys. Lett. A 213 (1996), 279-287.
[15] A. M. Wazwaz, Solutions of compact and noncompact structures for
nonlinear Klein-Gordon-type equation, Appl. Math. Comput. 134 (2003),
487-500.
[16] A. M. Wazwaz, A sine-cosine method for handling nonlinear wave
equations, Math. Comput. Model. 40 (2004), 499-508.
[17] A. M. Wazwaz, A reliable treatment of the physical structure for
the nonlinear equation K(m, n), Appl. Math. Comput. 163
(2005), 1081-1095.
[18] A. M. Wazwaz, A class of nonlinear fourth order variant of a
generalized Camassa-Holm equation with compact and noncompact
solutions, Appl. Math. Compt. 165 (2005), 485-501.
[19] A. M. Wazwaz, Solitons and periodic solutions for the fifth-order
KdV equation, Appl. Math. Lett. 19 (2006), 1162-1167.
[20] Z. Y. Yan, New explicit travelling wave solutions for two new
integrable coupled nonlinear evolution equations, Phys. Lett. A 292
(2001), 100-106.
[21] S. Zhang, New exact solutions of the KdV-Burgers-Kuramoto
equation, Phys. Lett. A 358 (2006), 414-420.
[22] Y. Zheng, S. Lai and Peakons, Solitary patterns and periodic
solutions for generalized Camassa-Holm equations, Phys. Lett. A 372
(2008), 4141-4143.
