Journal of Mathematical Sciences: Advances and Applications[1] G. A. Afrouzi and S. Heidarkhani, Three solutions for a Dirichlet
boundary value problem involving the p-Laplacian, Nonlinear
Anal. 66 (2007), 2281-2288.
[2] G. A. Afrouzi and S. Heidarkhani, Three solutions for a
quasilinear boundary value problem, Nonlinear Anal. 69(1-10)
(2008),3330-3336.
[3] G. Bonanno and P. Candito, Three solutions to a Neumann problem
for elliptic equations involving the p-Laplacian, Arch. Math.
(Basel) 80 (2003), 424-429.
[4] G. Cordaro and G. Raob, Three solutions for a perturbed Dirichlet
problem, Nonlinear Anal. 68 (2008), 3879-3883.
[5] D. E. Edmunds and J. RákosnÃk, Density of smooth
functions in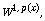 
Proc. R. Soc. Lond. Ser. A 437 (1992),
229-236.
[6] D. E. Edmunds, J. Lang and A. Nekvinda, On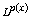 
norms, Proc. R. Soc. Lond. Ser. A 455
(1999), 219-225.
[7] D. E. Edmunds and J. RákosnÃk, Sobolev embedding with
variable exponent, Studia Math. 143 (2000), 267-293.
[8] X. L. Fan and D. Zhao, On the generalized Orlicz-Sobolev space
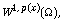J. Gansu Educ. College 12(1) (1998), 1-6.
[9] X. L. Fan, J. Shen and D. Zhao, Sobolev embedding theorems for
spaces 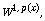J. Math. Anal. Appl. 262 (2001), 749-760.
[10] X. L. Fan and D. Zhao, On the spaces 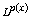and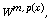 
J. Math. Anal. Appl. 263 (2001), 424-446.
[11] X. L. Fan and Q. H. Zhang, Existence of solutions for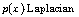 
Dirichlet problem, Nonlinear Anal. 52
(2003), 1843-1852.
[12] X. L. Fan and X. Y. Han, Existence and multiplicity of solutions
for 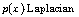equations in 
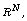Nonlinear Anal. 59 (2004), 173-188.
[13] O. KováÄik and J. RákosnÃk, On spaces
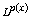and 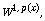Czechoslovak Math. J. 41 (1991), 592-618.
[14] Qiao Liu, Existence of three solutions for 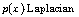equations, Nonlinear Anal. 68 (2008),
2119-2127.
[15] Mihai Mihailescu, Existence and multiplicity of solutions for a
Neumann problem involving the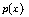 
-Laplace operator, Nonlinear Anal. 67 (2007),
1419-1425.
[16] M. Mihâilescu and V. Radulescu, A multiplicity result for a
nonlinear degenerate problem arising in the theory of
electrorheological fluids, Proc. R. Soc. Lond. Ser. A 462 (2006),
2625-2641.
[17] J. Musielak, Orlicz Spaces and Modular Spaces, Lecture Notes in
Mathematics, vol. 1034, Springer, Berlin, (1983).
[18] B. Ricceri, Existence of three solutions for a class of elliptic
eigenvalue problem, Math. Comput. Modelling 32 (2000), 1485-1494.
[19] B. Ricceri, A three critical points theorem revisited, Nonlinear
Anal. 70(9) (2009), 3084-3089.
