[1] M. Wadati, Stochastic Korteweg-de Vries equation, J. Phys. Soc.
Jpn. 52 (1983), 2642-2648.
[2] Y. C. Xie, Exact solutions for stochastic KdV equations, Phys.
Lett. A 310 (2003), 161-167.
[3] B. Chen and Y. C. Xie, Exact solutions for Wick-type stochastic
coupled Kadomtsev-Petviashili equations, J. Phys. A: Math. Gen. 38
(2005), 815-822.
[4] B. Chen and Y. C. Xie, Exact solutions for generalized stochastic
Wick-type KdV-mKdV equations, Chaos, Solitons and Fractals 23 (2005),
281-288.
[5] B. Chen and Y. C. Xie, White noise functional solutions of
Wick-type stochastic generalized Hirota-Satsuma coupled KdV equations,
J. Comput. Appl. Math. 197 (2006), 345-354.
[6] B. Chen and Y. C. Xie, Periodic-like solutions of variable
coefficients and Wick-type stochastic NLS equations, 203 (2007),
249-263.
[7] Y. C. Xie, An auto-Bäcklund transformation and exact solutions
for Wick-type stochastic generalized KdV equations, J. Phys. A: Math.
Gen. 37 (2004), 5229-5236.
[8] Y. C. Xie, Positonic solutions for Wick-type stochastic KdV
equations, Chaos, Solitons and Fractals 20 (2004), 337-342.
[9] Y. C. Xie, Exact solutions of the Wick-type stochastic
Kadomtsev-Peviashvili equations, Chaos, Solitons and Fractals 21
(2004), 473-480.
[10] H. A. Ghany. Exact solutions for stochastic generalized
Hirota-Satsuma coupled KdV equations. Chin. J. Phys. 49 (2011),
926-940.
[11] H. A. Ghany, Exact solutions for KdV-Burger equations with an
application of white-noise analysis, International Journal of Pure and
Applied Mathematics 78 (2012), 17-27.
[12] H. A. Ghany, Analytical approach to exact solutions for the
Wick-type stochastic space-time fractional KdV equation, Chin. Phys.
Lett. 31 (2014), 060503.
[13] H. A. Ghany, A. S. Okb El Bab, A. M. Zabal and A. Hyder, The
fractional coupled KdV equations: Exact solutions and white noise
functional approach, Chin. Phys. B 22 (2013), 0805011.
[14] H. A. Ghany and A. Hyder, White noise functional solutions for
Wick-type stochastic coupled KdV equations, Journal of Mathematical
Sciences: Advances and Applications 11 (2011), 79-96.
[15] H. A. Ghany and A. Hyder, White noise functional solutions for
the Wick-type two-dimensional stochastic Zakharov-Kuznetsov equations,
Int. Rev. Phys. 6 (2012), 153-157.
[16] H. A. Ghany and A. Hyder, Local and global well-posedness of
stochastic Zakharov-Kuznetsov equation, J. Comput. Anal. Appl. 15
(2013), 1332-1343.
[17] H. A. Ghany and A. Hyder, Exact solutions for the Wick-type
stochastic time-fractional KdV equations, Kuwait Journal of Science 41
(2014), 75-84.
[18] H. A. Ghany and A. Hyder, Abundant solutions of Wick-type
stochastic fractional 2D KdV equation, Chin. Phys. B 23 (2014),
060503.
[19] H. A. Ghany, A. Hyder and M. Zakarya, Non-Gaussian white noise
functional solutions of 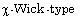 stochastic KdV equations, Appl. Math. Inf.
Sci., Accepted (2017).
stochastic KdV equations, Appl. Math. Inf.
Sci., Accepted (2017).
[20] A. Hyder and M. Zakarya, Non-Gaussian Wick calculus based on
hypercomplex systems, International Journal of Pure and Applied
Mathematics 109 (2016), 539-556.
[21] S. Albeverio, Yu. G. Kondratev and L. Streit, How to generalize
white noise analysis to non-Gaussian spaces, in: Dynamics of Complex
and Irregular Systems, World Scientific, Singapore (1993), 48-60.
[22] Y. Kondratiev, J. L. DA Silva and L. Streit, Generalized Appell
system, Meth. Funct. Anal. Topol. 3 (1997), 28-61.
[23] Y. Kondratiev, J. L. DA Silva, L. Streit and G. US, Analysis on
Poisson and gamma spaces, Infin. Dim. Anal. Quantum Probab. Relat.
Top. 1 (1998), 91-117.
[24] B. A. Løkka, B. Øksendal and F. Proske, Stochastic partial
differential equations driven by Lévy space-time white noise, The
Annals of Applied Probability 14 (2004), 1506-1528.
[25] B. Øksendal, Stochastic partial differential equations driven
by multi-parameter white noise of Lévy processes, Quart. Appl.
Math. 66 (2008), 521-537.
[26] H. Holden, B. Øksendal, J. Ubøe and T. Zhang, Stochastic
Partial Differential Equations, Springer Science+Business Media, LLC,
2010.
[27] A. de Bouard and A. Debussche, On the stochastic Korteweg-de
Vries Equation, J. Funct. Anal. 154 (1998), 215-251.
[28] M. L. Wang, Y. M. Wang, A new Bäcklund transformation and
multi-soliton solutions to the KdV equation with general variable
coefficients, Phys. Lett. A 287 (2001), 211-216.
[29] C. S. Gardner, J. M. Greene, M. D. Kruskal and R. M. Miura,
Method for solving the KdV equation, Phys. Rev. Lett. 19 (1967),
1095-1097.
[30] S. K. Liu, Q. Zhao, Z. T. Fu and S. D. Liu, Expansion method
about the Jacobi elliptic function and its applications to nonlinear
wave equations, Acta Phys. Sin. 50 (2001), 2068-2073.
[31] B. Øksendal and F. Proske, White noise of Poisson random
measures, Potential Anal. 21 (2004), 375-403.
[32] Z. X. Wang and D. R. Guo, Introduction to Special Functions,
Peking University Press: China, 2000.