References

Journal of Mathematical Sciences: Advances and Applications

DIRECT AND INVERSE TASK FOR THE OPERATOR STURM-LIOUVILLE TYPE WITH LINEAR DELAY

[1] G. Freiling and V. Yurko, Inverse Sturm-Liouville Problems and their Applications, Nova Science Publishers, Inc. Huntington, New York, 2008.

[2] M. G. Fasimov and B. M. Levitan, Determination of a differential equation by two spectra, UMN. (1964)-T(19). No 2. (116). 3-63.

[3] I. M. Gelfand and B. M. Levitan, Determination of a differential equation by its function spektralno. Izv. АN SSSR Ser.Мат-(1951).T.15.-S. 309-360.

[4] Göran Borg, Eine Umkehrung der Strum-Liouvilleschen Eigenwertaufgabe, Acta Math. 78-(1946), 1-96.

[5] M. Pikula, A differential operator of Sturm-Liouville problem with delay of two spectra, Bulletin Mathematica 43 (1991), 159-171.

[6] M. Pikula and T. Marjanovi, The construction of the small potential for an equation of Sturm-Liouville type with constant delay, Mathematical Conference in Pristin (1996), 135-141.

[7] R. I Lazovic and M. Pikula, Regularized trace of the operator applied to solving inverse problems, Radovi Matematicki, 2002.

[8] M. Pikula, On the determination equation of a differential with variable delay equation, Mathematica Montisnigri VI (1996).

[9] V. Vladicic, Doctoral thesis, University of East Sarajrevo, 2013. god.

[10] M. Pikula and I. Kalco, Eigenvalues operator Sturm-type Liouville with variable delay type of 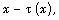Proceedings of the Second Mathematical Conference of the Republic of Srpska, (2012), 73-85.

[11] M. Pikula and I. Kalco, Design solutions border task with linear delay, Proceedings of the Third Mathematical Conference of the Republic of Srpska, (2013).

[12] I. Kalco, Construction solutions differential operator type Sturm –Liouville border task with linear delay, Bulletin of the international mathematical virtual institute ISSN (p) 2303-4874, ISSN (o) 2303-4955, 0.951.

[13] I. Kalco, M. Pikula and V. Miletic, Relations between the Fourier coefficients of transition function operator Sturm-type Liuvila with linear delay and own values of these operators, Proceedings of the Fourth Mathematical Conference of the Republic of Srpska, (2014), 383-394.