Journal of Mathematical Sciences: Advances and Applications[1] R. Baker, Lebesgue measure on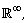 
II Proc. Amer. Math. Soc. 132 (9), (2004),
2577-2591.
[2] J. P. R. Christensen, Measure theoretic zero sets in infinite
dimensional spaces and applications to differentiability of Lipschitz
mappings, Actes du Deuxime Colloque d’Analyse Fonctionnelle de
Bordeaux (Univ. Bordeaux, 1973), I, pp. 29-39, Publ. Dp. Math. (Lyon)
10(2) (1973), 29-39.
[3] R. Dougherty, Examples of non-shy sets, Fund. Math. 144 (1994),
73-88.
[4] P. R. Halmos, Measure Theory, Princeton, Van Nostrand, (1950).
[5] B. Hunt, T. Sauer and J. Yorke, Prevalence: a
translation-invariant almost every on infinite-dimensional spaces,
Bull. Amer. Math. Soc. 27 (1992), 217-238.
[6] Hun Hee Lee, Vector valued Fourier analysis on unimodular groups,
Math. Nachr. 279(8) (2006), 854-874.
[7] J. Mycielski, Some unsolved problems on the prevalence of
ergodicity, instability, and algebraic independence, Ulam Quart. 1(3)
(1992), 30 ff., approx. 8 pp.
[8] G. R. Pantsulaia, On generators of shy sets on Polish topological
vector spaces, New York J. Math. 14 (2008), 235-259.
[9] G. R. Pantsulaia, Change of variable formula for Lebesgue measures
on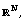 
J. Math. Sci.: Adv. Appl., Scientific
Advances Publishers 2(1) (2009), 1-12.
[10] C. A. Rogers, Hausdorff Measures, Cambridge Univ. Press,
(1970).
[11] Hongjia Shi, Measure-Theoretic Notions of Prevalence, Ph.D.
Dissertation (under Brian S. Thomson), Simon Fraser University (1997),
ix+165 pages.
[12] F. J. Hoffmann- Analytic Spaces and Their Application, C. A.
Rogers (et al.), Analytic Sets, Academic Press, London, (1980),
317-401.
