Journal of Mathematical Sciences: Advances and Applications
LAPLACIAN SYSTEMS[1] K. Adriouch and A. El Hamidi, The Nehari manifold for systems of
nonlinear elliptic equations, Nonlinear Anal. 64(10) (2006),
2149-2167.
[2] K. Adriouch, On Quasilinear and Anisotropic Elliptic Systems with
Sobolevs Critical Exponents, PhD Dissertation, Univ. of La Rochelle,
France, (2007).
[3] K. Adriouch and A. El Hamidi, On local compactness in quasilinear
elliptic problems, Diff. and Int. Equ. 20(1) (2007), 77-92.
[4] A. Ahammou, A multiplicity result for a quasilinear gradient
elliptic system, J. Appl. Math. 1(3) (2001), 91-106.
[5] A. Ahammou, On the existence of bounded solutions of nonlinear
elliptic systems, IJMMS 30(8) (2002), 479-490.
[6] C. O. Alves and A. El Hamidi, Nehari Manifold and Existence of
Positive Solutions to a Class of Quasilinear Problems, (1997).
[7] C. O. Alves, Multiple positive solutions for equations involving
critical Sobolev exponent in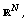 
Electron. J. Differ. Equ. 1997(13) (1997),
1-10.
[8] C. O. Alves, D. C. de Morais Filho and M. A. S. Souto, On systems
of elliptic equations involving subcritical or critical Sobolev
exponents, Nonlinear Anal. T. M. A. 42(5) (2000), 771-787.
[9] H. Brezis and E. Lieb, A relation between pointwise convergence of
functions and convergence of functionals, Proc. Amer. Math. Soc. 88
(1983), 486-490.
[10] C. N. Chen and S. Y. Tzeng, Some properties of
Palais–Smale sequences with applications to elliptic
boundary-value problems, Electron. J. Differ. Equ. 1999(17) (1999),
1-29.
[11] H. Egnell, Existence and nonexistence results for
m-Laplacian equations involving critical Sobolev exponents,
Arch. Rational Mech. Anal. 104 (1988), 57-77.
[12] I. Ekeland, Convexity Methods in Hamiltonian Mechanics, Springer,
(1990).
[13] G. Talenti, Best Constant in Sobolev Inequality, Ann. Math. 110
(1976), 353-372.
[14] J. Velin, Existence results for some nonlinear elliptic system
with lack of compactness. Nonlinear Anal. 52(3) (2003), 1017-1034.
