Journal of Mathematical Sciences: Advances and Applications
[1] S. R. Ashoka, C. S. Bagewadi and G. Ingalahalli, Certain results
on Ricci solitons in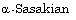 
manifolds, Hindawi Publ. Corporation,
Geometry, Vol. 2013, Article ID 573925, 4 pages.
[2] S. R. Ashoka, C. S. Bagewadi and G. Ingalahalli, A geometry on
Ricci solitons in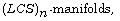 
Diff. Geom.-Dynamical Systems 16 (2014),
50-62.
[3] M. Atceken, On geometry of submanifolds of 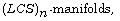Int. J. Math. and Math. Sci., 2012,
doi:10.1155/2012/304647.
[4] M. Atceken and S. K. Hui, Slant and pseudo-slant submanifolds of
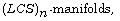Czechoslovak Math. J. 63 (2013),
177-190.
[5] C. S. Bagewadi and G. Ingalahalli, Ricci solitons in
Lorentzian-Sasakian manifolds, Acta Math. Acad. Paeda. Nyire. 28
(2012), 59-68.
[6] C. L. Bejan and M. Crasmareanu, Ricci solitons in manifolds with
quasi constant curvature, Publ. Math. Debrecen 78 (2011), 235-243.
[7] A. M. Blaga,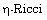 
solitons on para-Kenmotsu manifolds,
Balkan J. Geom. Appl. 20 (2015), 1-13.
[8] E. Cartan, Sur une classe remarquable d’espaces de
Riemannian, Bull. Soc. Math. France, 54 (1926), 214-264.
[9] M. C. Chaki, On pseudo-symmetric manifolds, An. Sti. Ale Univ. AL.
I. CUZA Din Iasi, 33 (1987), 53-58.
[10] M. C. Chaki, On pseudo Ricci symmetric manifolds, Bulg. J. Phys.
15 (1988), 526-531.
[11] M. C. Chaki, On generalized pseudo-symmetric manifolds, Publ.
Math. Debrecen 45 (1994), 305-312.
[12] S. Chandra, S. K. Hui and A. A. Shaikh, Second order parallel
tensors and Ricci solitons on 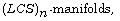Commun. Korean Math. Soc. 30 (2015),
123-130.
[13] B. Y. Chen and S. Deshmukh, Geometry of compact shrinking Ricci
solitons, Balkan J. Geom. Appl. 19 (2014), 13-21.
[14] U. C. De and S. Bandyopadhyay, On weakly symmetric Riemannian
spaces, Publ. Math. Debrecen 54 (1999), 377-381.
[15] U. C. De and A. A. Shaikh, Differential Geometry of Manifolds,
Narosa Publishing House Pvt. Ltd., New Delhi, 2007.
[16] S. Deshmukh, H. Al-Sodais and H. Alodan, A note on Ricci
solitons, Balkan J. Geom. Appl. 16 (2011), 48-55.
[17] R. Deszcz, On pseudo-symmetric spaces, Bull. Soc. Math. Belg.
Sér. A 44(1) (1992), 1-34.
[18] R. Deszcz, On Ricci-pseudosymmetric warped products, Demonstratio
Math. 22 (1989), 1053-1065.
[19] R. S. Hamilton, Three-manifolds with positive Ricci curvature, J.
Diff. Geom. 17 (1982), 255-306.
[20] R. S. Hamilton, The Ricci flow on surfaces, Mathematics and
General Relativity, Contemp. Math., 71, American Math. Soc. (1988),
237-262.
[21] S. K. Hui, On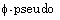 
symmetries of 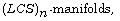Kyungpook Math. J. 53 (2013),
285-294.
[22] S. K. Hui and M. Atceken, Contact warped product semi-slant
submanifolds of 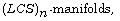Acta Univ. Sapientiae Mathematica 3(2)
(2011), 212-224.
[23] G. Ingalahalli and C. S. Bagewadi, Ricci solitons in 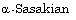manifolds, ISRN Geometry, Vol. 2012,
Article ID 421384, 13 pages.
[24] H. Levy, Symmetric tensors of the second order whose covariant
derivatives vanish, Annals of Math. 27 (1926), 91-98.
[25] K. Matsumoto, On Lorentzian almost paracontact manifolds, Bull.
of Yamagata Univ. Nat. Sci. 12 (1989), 151-156.
[26] I. Mihai and R. Rosca, On Lorentzian para-Sasakian manifolds,
Classical Anal., World Sci. Publ., Singapore, (1992), 155-169.
[27] H. G. Nagaraja and C. R. Premlatta, Ricci solitons in Kenmotsu
manifolds, J. Math. Analysis 3 (2012), 18-24.
[28] D. Narain and S. Yadav, On weak concircular symmetries of
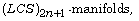Global J. Sci. Frontier Research 12
(2012), 85-94.
[29] B. O’Neill, Semi Riemannian Geometry with Applications to
Relativity, Academic Press, New York, 1983.
[30] E. M. Patterson, Some theorems on Ricci-recurrent spaces, J.
London Math. Soc. 27 (1952), 287-295.
[31] G. Perelman, The entropy formula for the Ricci flow and its
geometric applications, http://arXiv.org/abs/math/0211159, 2002,
1-39.
[32] G. Perelman, Ricci flow with surgery on three manifolds,
http://arXiv.org/abs/math/0303109, 2003, 1-22.
[33] D. G. Prakasha, On Ricci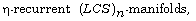 
Acta Univ. Apulensis 24 (2010),
109-118.
[34] A. Selberg, Harmonic analysis and discontinuous groups in weakly
symmetric Riemannian spaces with applications to Dirichlet series, J.
Indian Math. Soc. 20 (1956), 47-87.
[35] A. A. Shaikh, On Lorentzian almost paracontact manifolds with a
structure of the concircular type, Kyungpook Math. J. 43 (2003),
305-314.
[36] A. A. Shaikh, Some results on 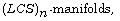J. Korean Math. Soc. 46 (2009),
449-461.
[37] A. A. Shaikh and H. Ahmad, Some transformations on 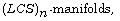Tsukuba J. Math. 38 (2014), 1-24.
[38] A. A. Shaikh and K. K. Baishya, On concircular structure
spacetimes, J. Math. Stat. 1 (2005), 129-132.
[39] A. A. Shaikh and K. K. Baishya, On concircular structure
spacetimes II, American J. Appl. Sci. 3(4) (2006), 1790-1794.
[40] A. A. Shaikh, T. Basu and S. Eyasmin, On locally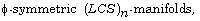 
Int. J. of Pure and Appl. Math. 41(8)
(2007), 1161-1170.
[41] A. A. Shaikh, T. Basu and S. Eyasmin, On the existence of
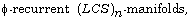Extracta Mathematicae 23(1) (2008),
71-83.
[42] A. A. Shaikh and T. Q. Binh, On weakly symmetric 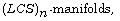J. Adv. Math. Studies 2 (2009), 75-90.
[43] A. A. Shaikh and S. K. Hui, On generalized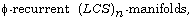 
AIP Conf. Proc. 1309 (2010), 419-429.
[44] A. A. Shaikh, Y. Matsuyama and S. K. Hui, On invariant
submanifold of 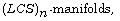J. of Egyptian Math. Soc. (2015).
[45] R. Sharma, Second order parallel tensor in real and complex space
forms, International J. Math. and Math. Sci. 12 (1989), 787-790.
[46] R. Sharma, Second order parallel tensor on contact manifolds,
Algebras, Groups and Geometrics 7 (1990), 787-790.
[47] R. Sharma, Certain results on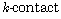 
and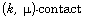 
manifolds, J. of Geom. 89 (2008),
138-147.
[48] Z. I. Szabó, Structure theorems on Riemannian spaces
satisfying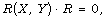 
The local version, J. Diff. Geom. 17
(1982), 531-582.
[49] L. Tamássy and T. Q. Binh, On weakly symmetric and weakly
projective symmetric Riemannian manifolds, Coll. Math. Soc. J. Bolyai
56 (1989), 663-670.
[50] L. Tamássy and T. Q. Binh, On weak symmetrics of Einstein and
Sasakian manifolds, Tensor N. S. 53 (1993), 140-148.
[51] M. M. Tripathi, Ricci solitons in contact metric manifolds,
arxiv:0801.4221 [Math.DG] (2008).
[52] K. Yano, Concircular geometry I, concircular transformations,
Proc. Imp. Acad. Tokyo 16 (1940), 195-200.
[53] A. G. Walker, On Ruses spaces of recurrent curvature, Proc.
London Math. Soc. 52 (1950), 36-64.
