Journal of Mathematical Sciences: Advances and Applications
DATA[1] E. Azroul, A. Barbara, M. B. Benboubker and S. Ouaro, Renormalized
solutions for a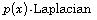 
equation with Neumann nonhomogeneous
boundary conditions and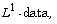 
Annals of Univ. of Craiova, Mathematics
and Computer Science Series 40 (2013), 9-22.
[2] M. Bendahmane and P. Wittbold, Renormalized solutions for
nonlinear elliptic equations with variable exponents and 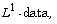Nonlinear Analysis TMA 70(2) (2009),
567-583.
[3] K. Bonzi Bernard, I. Nyanquini and S. Ouaro, Existence and
uniqueness of weak and entropy solutions for homogeneous Neumann
boundrary-value problems involving variable exponents, Electronic
Journal of Differential Equations 12 (2012), 1-19.
[4] L. Boccardo and T. Gallouët, Nonlinear elliptic equations with
right hand side measures, Comm. Partial Differential Equations 17
(1992), 641-655.
[5] L. Boccardo, T. Gallouët and L. Orsina, Existence and
uniqueness of entropy solutions for nonlinear elliptic equations with
measure data, Ann. Inst. H. Poincaré Anal. Non Linéaire 13(5)
(1996), 539-551.
[6] Y. Chen, S. Levine and M. Rao, Variable exponent, linear growth
functionals in image restoration, SIAM J. Appl. Math. 66 (2006),
1383-1406.
[7] L. Diening, P. Harjulehto, P. Hästö and M. Ruzicka, Lebesgue
and Sobolev Spaces with Variable Exponents, Vol. 2017 of Lecture Notes
in Mathematics, Springer, 2011.
[8] D. Edmunds and J. Rakosnik, Sobolev embeddings with variable
exponent, Studia Math. 143 (2000), 267-293.
[9] X. L. Fan and D. Zhao, On the spaces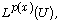 
and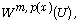 
J. Math. Anal. Appl. 263 (2001),
424-446.
[10] P. Harjulehto, P. Hästö, M. Koskenoja and S. Varonen, The
Dirichlet energy integral and variable exponent sobolev spaces with
zero boundary values, Potential Analysis 25(3) (2006), 205-222.
[11] B. Lv, F. Li and W. Zou, Existence of weak solutions for some
nonlinear elliptic equations with variable exponents, Complex
Variables and Elliptic Equations 58 (2013), 1431-1447.
[12] J.-L. Lions, Quelques Méthodes de Résolution des
Problémes aux Limites non Linéaires, Dunod, 1969.
[13] M. Mihailescu and V. Radulescu, A multiplicity result for a
nonlinear degenrate problem arising in the theory of
eletro-rheological fluids, Proc. R. Soc. A. 462 (2006), 2625-2641.
[14] K. Rajagopal and M. Ruzicka, Mathematical modelling of
electro-rheological fluids, Contin. Mech. Thermodyn. 13 (2001),
59-78.
[15] M. Ruzicka, Electrorheological fluids: Modeling and Mathematical
Theory, Springer, Berlin, Lecture Notes in Mathematics 1748, 2000.
[16] M. Sanchon and J. M. Urbano, Entropy solutions for the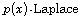 
equation, Trans. Amer. Math. Soc. 361
(2009), 6387-6405.
[17] C. Zhang and S. Zhou, Entropy and renormalized solutions for the
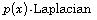equation with measure data, Bull. Aust.
Math. Soc. 82 (2010), 459-479.
[18] C. Zhang, Entropy solutions for nonlinear elliptic equations with
variable exponents, Electronic Journal of Differential Equations 92
(2014), 1-14.
