Journal of Mathematical Sciences: Advances and Applications[1] P. Auscher and P. Tchamitchian, Square root problem for divergence
operators and related topics, Asterisque 249 (1998), 1-172.
[2] P. Auscher, S. Hofmann, M. Lacey, A. Mcintosh and Ph.
Tchamitchian, The solution of the Kato square root problem for second
order elliptic operators on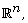 
Ann. of Math. 156(2) (2002), 633-654.
[3] C. Bennett and R. Sharpley, Interpolation of Operators, 129, Pure
and Applied Mathematics, Academic Press, Inc., Boston, MA, 1988.
[4] D. G. Deng, X. T. Duong, A. Sikora and L. X. Yan, Comparison of
the classical BMO with the BMO spaces associated with operators and
applications, Rev. Mat. Iberoam. 24(1) (2008), 267-296.
[5] X. T. Duong and L. X. Yan, Duality of Hardy and BMO spaces
associated with operators with heat kernel bounds, Amer. J. Math. 18
(2005), 943-973.
[6] X. T. Duong and L. X. Yan, New function spaces of BMO type,
John-Nirenberg inequality, interpolation and applications, Comm. Pure
Appl. Math. 58 (2005), 1375-1420.
[7] M. Frazier and B. Jawerth, A discrete transform and decompositions
of distributional spaces, J. Funct. Anal. 93 (1990), 34-170.
[8] H. Kozono and H. Wadade, Remarks on Gagliardo-Nirenberg type
inequality with critical Sobolev space and BMO, Math. Z. 259(4)
(2008), 935-950.
[9] Alan Mcintosh, Operators which have an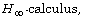 
Miniconference on operator theory and
partial differential equations, Proc. Center. Math. Analysis ANU,
Canberra, 14 (1986), 210-231.
[10] Z. Shen, On fundamental solution of generalized Schrödinger
operators, J. Funct. Anal. 167 (1999), 521-564.
[11] N. T. Varopoulos, L. Saloff-Coste and T. Coulhon, Analysis and
Geometry on Groups, Cambridge Tracts in Mathematics, 100, Cambridge
University Press, Cambridge, 1992.
