Journal of Mathematical Sciences: Advances and Applications[1] O. Aberth, Iteration methods for finding all zeros of a polynomial
simultaneously, Math. Comput. 27 (1973), 339-344.
[2] E. Durand, Solution Numériques des Équations
Algébraiques, Tom. I: Équations du Type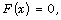 
Racines d’un Polynôme, Masson,
Paris, 1960.
[3] P. Henrici, Applied and Computational Complex Analysis, Vol. 1,
John Wiley and Sons Inc., New York, 1974.
[4] I. O. Kerner, Ein Gesamtschrittverfahren zur Berechnung der
Nullstellen von Polynomen, Numer. Math. 8 (1966), 290-294.
[5] M. S. Petković, D. Herceg and I. Petković, On a
simultaneous method of Newton-Weierstrass\\\\\\\\\\\\\\\' type for
finding all zeros for a polynomial, Appl. Math. Comput. 215 (2009),
2456-2463.
[6] M. S. Petković and L. D. Petković, On a cubically
convergent derivative free root finding method, Int. J. Comput. Math.
84 (2007), 505-513.
[7] J. F. Traub, Iterative Methods for the Solution of Equations,
Prentice-Hall, Englewood Cliffs, New Jersey, 1964.
[8] S. Weerakoon and T. G. I. Fernando, A variant of Newton’s
method with accelerated third-order convergence, Appl. Math. Lett. 13
(2000), 87-93.
