Journal of Mathematical Sciences: Advances and Applications[1] F. E. Browder, Fixed-point theorems for noncompact mappings in
Hilbert space, Proc. Natl. Acad. Sci. USA 53 (1965), 1272-1276.
[2] R. E. Bruck, On the convex approximation property and the
asymptotic behavior of nonlinear contractions in Banach spaces, Israel
J. Math. 38 (1981), 304-314.
[3] R. E. Bruck, A simple proof of the mean ergodic theorem for
nonlinear contractions in Banach spaces, Israel J. Math. 32 (1979),
107-116.
[4] R. Chen, Y. Song and H. Zhou, Convergence theorems for implicit
iteration process for a finite family of continuous pseudocontractive
mappings, J. Math. Anal. Appl. 314 (2006), 701-709.
[5] R. Chen, Y. Song and H. Zhou, Viscosity approximation methods for
continous pseudo-contractive mappings, Acta Mathematica Sinica,
Chinese series 49 (2006), 1275-1278.
[6] C. E. Chidume and E. U. Ofoedu, A new iteration process for
generalized Lipschitz pseudo-contractive and generalized Lipschitz
accretive mappings, Nonlinear Anal. 67 (2007), 307-315.
[7] C. E. Chidume and C. O. Chidume, Iterative approximation of fixed
points of nonexpansive mappings, J. Math. Anal. Appl. 318 (2006),
288-295.
[8] C. E. Chidume and S. A. Mutangadura, An example on the Mann
iteration method for Lipschitz pseudocontractions, Proc. Amer. Math.
Soc. 129(8) (2001), 2359-2363.
[9] C. E. Chidume and C. Moore, Fixed point iteration for
pseudo-contractive maps, Proc. Amer. Math. Soc. 127(4) (1999),
1163-1170.
[10] C. E. Chidume, Global iteration schemes for strongly
pseudo-contractive maps, Proc. Amer. Math. Soc. 126(9) (1998),
2641-2649.
[11] C. E. Chidume, Approximation of fixed points of strongly
pseudo-contractive mappings, Proc. Amer. Math. Soc. 120(2) (1994),
545-551.
[12] C. E. Chidume, Iterative approximation of Lipschitz strictly
pseudo-contractive mappings, Proc. Amer. Math. Soc. 99(2) (1987),
283-288.
[13] Y. J. Cho and X. Qin, Viscosity approximation methods for a
family of m-accretive mappings in reflexive Banach spaces, Positivity
(2008), DOI 10.1007/s11117-007-2181-8.
[14] K. Deimling, Zero of accretive operators, Manuscripta Math. 13
(1974), 365-374.
[15] L. Deng and X. P. Ding, Iterative approximation of Lipschitz
strictly pseudo-contractive mappings in uniformly smooth Banach
spaces, Nonlinear Anal. 24(7) (1995), 981-987.
[16] L. Deng, On chidumes open problems, J. Math. Anal. Appl. 174(2)
(1993), 441-449.
[17] T. L. Hicks and J. R. Kubicek, On the Mann iteration process in
Hilbert space, J. Math. Anal. Appl. 59 (1977), 498-504.
[18] T. H. Kim and H. K. Xu, Strong convergence of modified Mann
iterations, Nonlinear Anal. 61 (2005), 51-60.
[19] E. Kopecká and S. Reich, Nonexpansive retracts in Banach
spaces, Banach Center Publications 77 (2007), 161-174.
[20] L. S. Liu, Ishikawa and Mann iteration process with errors for
nonlinear strongly accretive mappings in Banach spaces, J. Math. Anal.
Appl. 194 (1995), 114-125.
[21] W. R. Mann, Mean value methods in iteration, Proc. Amer. Math.
Soc. 4 (1953), 506-510.
[22] C. H. Morales and J. S. Jung, Convergence of paths for
pseudo-contractive mappings in Banach spaces, Proc. Amer. Math. Soc.
128 (2000), 3411-3419.
[23] S. Reich, Strong convergence theorems for resolvents of accretive
operators in Banach spaces, J. Math. Anal. Appl. 75 (1980),
287-292.
[24] S. Reich, Weak convergence theorems for nonexpansive mappings in
Banach spaces, J. Math. Anal. Appl. 67 (1979), 274-276.
[25] S. Reich, Approximating zeros of accretive operators, Proc. Amer.
Math. Soc. 51 (1975), 381-384.
[26] S. Reich, Asymptotic behavior of contractions in Banach spaces,
J. Math. Anal. Appl. 44 (1973), 57-70.
[27] J. Schu, Approximating fixed points of Lipschitzian
pseudocontractive mappings, Houston J. Math. 19 (1993), 107-115.
[28] Y. Song and S. Xu, Strong convergence theorems for nonexpansive
semigroup in Banach spaces, J. Math. Anal. Appl. 338 (2008), 152-161.
[29] Y. Song and R. Chen, Strong convergence of an iterative method
for non-expansive mappings, Mathematische Nachrichten 281(8) (2008),
1196-1204.
[30] Y. Song, A note on the paper A new iteration process for
generalized Lipschitz pseudo-contractive and generalized Lipschitz
accretive mappings, Nonlinear Anal. 68 (2008), 3047-3049.
[31] Y. Song, On a Mann type implicit iteration process for continuous
pseudo-contractive mappings, Nonlinear Anal. 67 (2007), 3058-3063.
[32] Y. Song and R. Chen, Convergence theorems of iterative algorithms
for continuous pseudo-contractive mappings, Nonlinear Anal. 67 (2007),
486-497.
[33] Y. Song and R. Chen, An approximation method for continuous
pseudocontractive mappings, J. Inequal. Appl. (2006), 1-9.
[34] T. Suzuki, Strong convergence of approximated sequences for
nonexpansive mappings in Banach spaces, Proc. Amer. Math. Soc. 135
(2007), 99-106.
[35] T. Suzuki, Strong convergence theorems for infinite families of
nonexpansive mappings in general Banach spaces, Fixed Point Theory and
Applications 2005(1) (2005), 103-123.
[36] W. Takahashi and Y. Ueda, On Reich’s strong convergence
for resolvents of accretive operators, J. Math. Anal. Appl. 104
(1984), 546-553.
[37] A. Udomene, Path convergence, approximation of fixed points and
variational solutions of Lipschitz pseudocontractions in Banach
spaces, Nonlinear Anal. 67 (2007), 2403-2414.
[38] H. K. Xu, Iterative algorithms for nonlinear operators, J. London
Math. Soc. 66 (2002), 240-256.
[39] H. K. Xu, Strong convergence of an iterative method for
nonexpansive and accretive operators, J. Math. Anal. Appl. 314 (2006),
631-643.
[40] H. Zhou, Convergence theorems for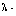 
strict pseudo-contractions in 2-uniformly
smooth Banach spaces, Nonlinear Analysis (2007), doi:10.1016/
j.na.2007.09.009.
