Journal of Mathematical Sciences: Advances and Applications[1] G. Bennett, Some elementary inequalities, Quart. J. Math. Oxford
38(2) (1987), 401-425; 39 (1988), 385-400; 42 (1991), 149-174.
[2] G. Bennett, Factorizing the classical inequalities, Memoirs Amer.
Math. Soc. 576 (1996), 1-130.
[3] G. Bennett, Inequalities complimentary to Hardy, Quart. J. Math.
Oxford 49(2) (1998), 395-432.
[4] D. Borwein and A. Jakimovski, Matrix operators on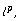 
Rocky Mountain J. Math. 9 (1979), 463-477.
[5] J. S. Bradley, Hardy inequality with mixed norms, Canad. Math.
Bull. 21 (1978), 405-408.
[6] Chang-Pao Chen, Dah-Chin Luor and Zong-Yin Ou, Extensions of Hardy
inequality, J. Math. Anal. Appl. 273 (2002), 160-171.
[7] Chang-Pao Chen, Hao-Wei Huang and Chun-Yen Shen, Matrices whose
norm are determined by its action on decreasing sequences, Canadian
Math. (to appear).
[8] L. W. Cohen and N. Dunford, Transformations on sequence spaces,
Duke J. Math. 3 (1937), 689-701.
[9] L. Crone, A characterization of matrix operators on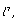 
Math. Z. 123 (1971), 315-317.
[10] G. H. Hardy, J. E. Littlewood and G. Polya, Inequalities, 2nd
edition, Cambridge Univ. Press, Cambridge, 1967.
[11] A. Jakimovski and D. C. Russell, Matrix mappings between
BK-spaces, Bull. London Math. Soc. 4 (1972), 345-353.
[12] G. J. O. Jameson, Norms and lower bounds of operators on the
Lorentz sequence space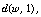 
Illinois J. Math. 43 (1999), 79-99.
[13] G. J. O. Jameson and R. Lashkaripour, Norms of certain operators
on weighted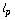 
spaces and Lorentz sequence spaces, JIPAM.
J. Inequal. Pure Appl. Math. 3(1) (2002), Article 6, pp. 17
(electronic).
[14] M. Koskela, A characterization of non-negative matrix operators
on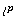 
to 
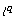with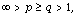 
Pacific J. Math. 75 (1978), 165-169.
[15] V. G. Maz’ja, Sobolev Spaces, Springer-Verlag, Springer
Series in Soviet Mathematics 1985.
[16] B. Muckenhoupt, Hardy inequality with weights, Studia Math. 44
(1972), 31-38.
[17] W. Rudin, Principles of Mathematical Analysis, 3rd ed.,
McGraw-Hill, New York, 1976.
[18] W. L. C. Sargent, Some sequence spaces related to the 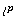spaces, J. London Math. Soc. 35 (1960),
161-171.
