Journal of Mathematical Sciences: Advances and Applications
[1] D. Burde, Lie algebra prederivations and strongly nilpotent Lie
algebras, Comm. in Algebra 30(7) (2002), 3157-3175.
[2] H. Chen and Y. Gao,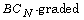 
Lie algebras arising from fermionic
representations, J. Algebra 308 (2007), 545-566.
[3] I. B. Frenkel, Spinor representations of affine Lie algebras,
Proc. Natl. Acad. Sci. 77 (1980), 6303-6306.
[4] A. J. Feingold and I. B. Frenkel, Classical affine algebras, Adv.
Math. 56 (1985), 117-172.
[5] J. R. Gómez, A. Jimenéz-Merchán and Y. Khakimdjanov,
Low-dimensional filiform Lie algebras, J. Pure Applied Algebra 130
(1998), 133-158.
[6] M. Goze and Y. Khakimdjanov, Nilpotent Lie Algebra, Mathematics
and its Applications, The Netherlands: Kluwer Academic Publishers, MIA
361 (1996).
[7] M. Hazewinkel, Handbook of Algebra, Vol. 2, CMI Amsterdam,
2000.
[8] P. Ji and L. Wang, Lie triple derivation of TUHF algebra, Linear
Algebra Appl. 403 (2005), 399-408.
[9] A. J. MartÃn and C. M. González, The Banach-Lie group of Lie
triple automorphisms of an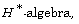 
Acta Math. Sci. Ser. B Engl. Ed. 30(4)
(2010), 1219-1226.
[10] S. Ou, D. Wang and R. Yao, Derivations of the Lie derivation of
strictly upper triangular matrices over a commutative ring, Linear
Algebra Appl. 424(2-3) (2007), 378-383.
[11] M. Vergne, Cohomologie des algèbres de Lie nilpotentes,
Application à l’étude de la variété des algèbres
de Lie nilpotentes’, Bull. Soc. Math. 98 (1970), 81-116.
[12] D. Wang and Q. Yu, Derivations of the parabolic subalgebras of
the general linear Lie algebra over a commutative ring, Linear Algebra
Appl. 416(2-3) (2006), 763-774.
[13] H. Wang and Q. Li, Lie triple derivation of the Lie algebra of
strictly upper triangular matrix over a commutative ring, Linear
Algebra Appl. 430(1) (2009), 66-77.
[14] J. Zhang and H. Cao, Lie triple derivation of nest algebra,
Linear Algebra Appl. 416(2-3) (2006), 559-567.
