Journal of Mathematical Sciences: Advances and Applications[1] M. J. Ablowitz and P. A. Clarkson, Solitons, Nonlinear Evolution
Equations and Inverse Scattering Transform, Cambridge University
Press, Cambridge, 1991.
[2] W. Maliet, Solitary wave solutions of nonlinear wave equations,
Am. J. Phys. 60 (1992), 650-654.
[3] W. Maliet, The tanh method: A tool for solving certain classes of
nonlinear evolution and wave equations, J. Comput. Appl. Math. 164
(156) (2004), 529-541.
[4] E. G. Fan, Extended tanh-function method and its applications to
nonlinear equations, Phys. Lett. A 277 (2000), 212-218.
[5] E. G. Fan and Y. C. Hong, Generalized tanh method to special types
of nonlinear equations, Z. Naturforsch. A 57 (2002), 692-700.
[6] M. Wang, Exact solutions for a compound KdV-Burgers equation,
Phys. Lett. A 213 (1996), 279-287.
[7] J. H. He and X. H. Wu, Exp-function method for nonlinear wave
equations, Chaos, Solitons Fractals 30 (2006), 700-708.
[8] A. M. Wazwaz, Variants of the generalized KdV equation with
compact and non-compact structures, Computers Mathematics with
Applications 47 (2004), 583-591.
[9] E. Yusufoglu, A. Bekir and M. Alp, Periodic and solitary wave
solutions of Kawahara and modified Kawahara equations by using
sine-cosine method, Chaos, Solitons Fractals 37 (2008), 1193-1197.
[10] Y. Peng, Exact periodic wave solutions to a new Hamiltonian
amplitude equation, J. Phys. Soc. Japan 72 (2003), 1356-1359.
[11] Y. Peng, New exact solutions to a new Hamiltonian amplitude
equation II, J. Phys. Soc. Japan 73 (2004), 1156-1158.
[12] Y. Peng, Exact periodic wave solutions to the Melnikov equation,
Z. Naturforsch. A 60 (2005), 321-327.
[13] Y. B. Zhao, M. L. Wang and Y. M. Wang, Periodic wave solutions to
a coupled KdV equations with variable coefficients, Phys. Lett. A 308
(2003), 31-36.
[14] J. Liu and K. Yang, The extended F-expansion method and
exact solutions of non-linear PDEs, Chaos, Solitons and Fractals 22
(2004), 111-121.
[15] H. T. Chen and H. Q. Zhang, New double periodic and multiple
soliton solutions of the generalized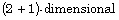 
Boussinesq equation, Chaos, Solitons and
Fractals 20 (2004), 765-769.
[16] S. A. Elwakil, S. K. El-labany, M. A. Zahran and R. Sabry,
Modified extended tanh-function method for solving nonlinear partial
differential equations, Phys. Lett. A 299 (2002), 179-188.
[17] M. A. Abdou and S. Zhang, New periodic wave solutions via
extended mapping method, Commun. Nonlinear Sci. Numer. Simul. 14
(2009), 2-11.
[18] D. Baldwin, U. Goktas and W. Hereman et al., Symbolic computions
of exact solutions expressible in hyperbolic and elliptic functions
for nonlinear PDEs, J. Symb. Comput. 37 (2004), 669-705.
[19] Taogetusang and Sirendaoerji, The Jacobi elliptic function-like
exact solutions to two kinds of KdV equations with variable
coefficients and KdV equation with forcible term, Chinese Phys. 15
(2006), 2809-2818.
[20] A. H. Khater, M. M. Hassan, E. V. Krishnan and Y. Z. Peng,
Applications of elliptic functions to ion-acoustic plasma waves, Eur.
Phys. J. D 50 (2008), 177-184.
[21] M. M. Hassan, New exact solutions of two nonlinear physical
models, Commun. Theor. Phys. China 53 (2010), 596-604.
[22] Hans Schamel, A modified Korteweg-de Vries equation for ion
acoustic wavess due to resonant electrons, Journal of Plasma Physics 9
(1973), 377-387.
[23] S. G. Tagare and A. Chakrabarti, Solution of a generalized
Korteweg-de Vries equation, Phys. Fluids A 17 (1974), 1331-1332.
[24] Willy A. Hereman and Takaoka Masanori, Solitary wave solutions of
nonlinear evolution and wave equations using a direct method and
MACSYMA, J. Phys. A: Math. Gen. 23 (1990), 4805-4822.
[25] Jonu Lee and Rathinasamy Sakthivel, Exact travelling wave
solutions of the Schamel-Korteweg-de Vries equation, Reports on
Mathematical Physics 68 (2011), 153-161.
[26] A. H. Khater and M. M. Hassan, Exact solutions expressible in
hyperbolic and Jacobi elliptic functions of some important equations
of ion-acoustic waves, Acoustic Waves-From Microdevices to
Helioseismology (2011), 67-78.
[27] Jian Yang, Ruizhi Shen and Shengqiang Tang, Exact Travelling wave
solutions for the 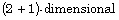generalized Camassa-Holm equation, Journal
of Pure and Applied Mathematics: Advances and Applications 3 (2010),
249-263.
[28] Jian Yang and Shengqiang Tang, Analytic solutions of the
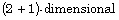nonlinear evolution equations using the
extended tanh method, Journal of Mathematical Sciences: Advances and
Applications 4 (2010), 359-369.
