Journal of Mathematical Sciences: Advances and Applications[1] A. M. Ilin and O. A. Oleinik, Asymptotic behavior of the solutions
of the Cauchy problem for certain quasilinear equations for large time
(in Russian), Mat. Sbornik 51 (1960), 191-216.
[2] T. P. Liu, Nonlinear stability of shock waves for viscous
conservation laws, Memoirs AMS 328 (1985), 1-108.
[3] K. Nishihara, A note on the stability of travelling wave solution
of Burger’s equation, Japan J. Appl. Math. 2 (1985), 27-35.
[4] S. Kawashima and A. Matsumura, Asymptotic stability of travelling
wave solutions of systems for one-dimensional gas motion, Comm. Math.
Phys. 101 (1985), 97-127.
[5] A. Matsumura and K. Nishihara, On the stability of travelling wave
solutions of a one-dimensional model system for compressible viscous
gas, Japan J. Appl. Math. 2 (1985), 17-25.
[6] J. Goodman, Nonlinear asymptotic stability of viscous shock
profiles for conservation laws, Arch. Rat. Mech. Anal. 95 (1986),
325-344.
[7] T. P. Liu and S. H. Yu, Propagation of a stationary shock layer in
the presence of a boundary, Arch. Rat. Mech. Anal. 139 (1997),
57-82.
[8] T. P. Liu and K. Nishihara, Asymptotic behavior for scalar viscous
conservation laws with boundary effect, J. Differential Equations 133
(1997), 296-320.
[9] T. P. Liu, A. Matsumura and K. Nishihara, Behavior of solutions
for the Burgers equations with boundary corresponding to rarefaction
waves, SIAM J. Math. Anal. 29 (1998), 293-308.
[10] K. Ito, Asymptotic decay toward the planar rarefaction waves of
solutions for viscous conservation laws in several dimensions, Math.
Models Methods Appl. Sci. 6 (1996), 315-338.
[11] S. Kawashima, S. Nishibata and M. Nishikama, Asymptotic stability
of stationary waves for two-dimensional viscous conservation laws in
half plane, Discrete and Continuous Dynamical Systems, Supplement,
(2003), 469-476.
[12] S. Kawashima, S. Nishibata and M. Nishikama,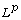 
energy method of multi-dimensional viscous
conservation laws and application to the stability of planar waves, J.
Hyperbolic Differential Equations 1 (2004), 581-603.
[13] T. Nakamura, Asymptotic decay toward the rarefaction waves of
solutions for viscous conservation laws in a one-dimension half space,
SIAM J. Math. Anal. 34 (2003), 1308-1317.
[14] M. Nishihara and K. Nishihara, Asymptotic toward the planar
rarefaction wave for viscous conservation law in two space dimensions,
Trans. Amer. Math. Soc. 352 (2000), 1203-1215.
[15] Z. P. Xin, Asymptotic stability of planar rarefaction waves for
viscous conservation laws in several dimensions, Trans. Amer. Math.
Soc. 319 (1990), 805-820.
[16] Z. P. Xin, Asymptotic stability of rarefaction waves for
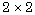viscous hyperbolic conservation laws-The
two modes case, J. Differential Equations 78 (1989), 191-219.
[17] L. L. Fan, H. X. Liu and H. Yin, Decay estimates of planar
stationary waves for damped wave equations with nonlinear convection
in multi-dimensional half space, Acta Math. Sci. 31(4) (2011),
1389-1410.
[18] K. Nishihara, Asymptotic behaviors of solutions to viscous
conservation laws via the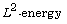 
method, Adv. Math. 304 (2001), 293-321.
